1-й тур: Задачи

1. Повышение квалификации

Компания Z может поставлять на конкурентный рынок два товара: ИКС и ИГРЕК. Цена товара ИКС равна 16 у.д.ед. (условные денежные единицы), а цена товара ИГРЕК равна 10 у.д.ед. В штате компании Z состоит 160 сотрудников одинаковой квалификации, каждый из которых подписывает годовой контракт с работодателем с заработной платой 0,4 у.д.ед. в год. За год любой сотрудник может произвести либо 0,05 единиц товара ИКС, либо 0,1 единиц товара ИГРЕК, при этом альтернативные издержки производства любого товара всегда постоянны. Годовая стоимость аренды помещения и оборудования для компании Z составляет 10 у.д.ед. Себестоимость производства каждой единицы любого товара (без учета расходов на оплату труда и аренду помещения и оборудования) постоянна и равна 1 у.д.ед. Считайте, что компания в состоянии контролировать работу сотрудников, и ни у кого из них нет стимула работать неэффективно.

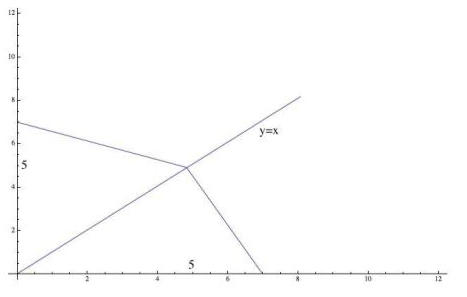
(а) Изобразите кривую производственных возможностей компании и найдите ее годовую прибыль.

(б) У компании есть возможность провести обучение на курсах повышения квалификации, обязательное для всех сотрудников. Стоимость курсов фиксированная и составляет 6 у.д.ед. независимо от числа обучающихся. При этом известно, что после обучения ровно четверть сотрудников незамедлительно повысит производительность своего труда в производстве товара ИКС на 50%. Производительность остальных работников не изменится. При этом компания Z будет вынуждена на 25% поднять годовую зарплату сотрудников, повысивших свою производительность. Изобразите новую кривую производственных возможностей компании. Станет ли компания проводить курсы повышения квалификации для всех сотрудников?

(в) Почему сотрудники могут быть заинтересованы в прохождении курсов повышения квалификации, даже если по их результатам не последует повышения заработной платы? Назовите экономическую концепцию, позволившую вам ответить на вопрос. На основе положений какой экономической концепции можно объяснить целесообразность данной политики для фирм (организовать курсы, полностью оплатить из средств компании, заработную плату сотрудникам не повышать)? Представьте экономическое обоснование выгод фирмы.

Решение

а)Кривая производственных возможностей описывается уравнением:
$$20X+10Y=160, \text{или } 2X+Y=16$$
Годовая зарплата сотрудников при производстве любого товара одинакова и себестоимость каждой единицы любого товара постоянна и равна $1$. Альтернативные издержки производства одной единицы товара X составляют $2$ единицы товара Y. При любых положительных объемах производства обоих товаров, отказавшись от производства одной единицы товара X компания сократит прибыль на $16-1=15$ у.д.ед., а произведя взамен $0.1/0.05=2$ единицы товара Y, компания увеличит прибыль на $10 \times 2 - 1 \times 2 = 18$ у.д.ед. Поэтому, максимизируя прибыль, компании необходимо специализироваться на производстве товара Y.

Прибыль компании Z в этом случае составит:
$(10-1) \times 160/10 - 0.4 \times 160-10=70$ у.д. ед.
На рисунке ниже $П_{0}=70+10.$

(б) Альтернативная стоимость производства одной единицы товара X теперь зависит от того, какое количество сотрудников, повысивших производительность после обучения, заняты в производстве этого товара. Если в производство дополнительной единицы товара Х вовлекаются сотрудники, сохранившие производительность неизменной, то альтернативные издержки производства одной единицы товара X составляют, как и прежде, $0.1/0.05=2$ единицы товара Y. Если же в производство дополнительной единицы товара X вовлекаются лишь сотрудники, повысившие свою производительность после обучения, то альтернативные издержки производства одной единицы товара X составляют $0.1/(0.05 \times 1.5)=4/3$ единиц товара Y. Если же в производство дополнительной единицы товара Х вовлекаются лишь сотрудники, повысившие свою производительность после обучения, то альтернативные издержки производства одной единицы товара Х составляют $0.1/(0.05 \times 1.5)=4/3 $ единиц товара Y. Кривая производственных возможностей показывает, какое максимальное количество одного товара может быть произведено при данном объеме производства другого товара. Чтобы построить кривую производственных возможностей, необходимо заметить, что при любом данном объеме производства товара Y максимальное количество товара Х будет произведено, только если в его производство будет вовлечено максимальное (из возможного) количество сотрудников, повысивших производительность в производстве товара Х. То есть, чтобы начать производство товара Х, следует использовать сначала технологический процесс, имеющий наименьшие альтернативные издержки производства этого товара. Только после того, как все сотрудники, повысившие свою производительность, будут вовлечены в производство товара Х (ими будет произведено $160 \times 0.25 \times 0.05 \times 1.5 = 3 $ единицы товара Х), следует использовать в производстве этого товара сотрудников, которые не повысили производительность по итогам проведения курсов (ими будет произведено $160 \times 0.75 \times 0.05 = 6 $ единиц товара Х).
Кривая производственных возможностей в этом случае:
\[ \left[\begin{array}
$\dfrac{4X}{3}+Y=16, & \text{ где } 0 \le X \le 3\\
2X+Y=18 , & \text{ где } 3< X \le 9
\end{array}\right.\]

Для максимизации своей прибыли вовлекать в производство любой дополнительной единицы товара Х сотрудников, не повысивших производительность, компании невыгодно, так как в этом случае компания увеличит прибыль от продажи этой единицы товара Х на $(16-1) \times 1 =15$ у.д.ед., и сократит прибыль от сокращения производства товара Y на $2$ единицы на $(10-1) \times 2=18$ у.д.ед. Если же не все сотрудники, повысившие производительность, заняты в производстве товара Х, то всегда выгодно увеличить его производство, поскольку увеличив производство товара Х на одну единицу, компания увеличит прибыль от продажи этой единицы товара на $(16-1) \times 1=15$ у.д.ед., и сократит прибыль от сокращения производства товара Y на $4/3$ единицы на $(10-1) \times 4/3 =12$ у.д.ед. Таким образом, наибольшую прибыль компания может получить, только если все сотрудники, которые повысили производительность после обучения, заняты в производстве товара Х, а все остальные – заняты в производстве товара Y. При этом прибыль компании составит:
$(16-1) \times 1.5 \times 40 \times 0.05 + (10-1) \times 120 \times 0.1 - 0.4 \times 1.25 \times 40 - 0.4 \times 120 - 10 - 6 =69$у.д.ед.
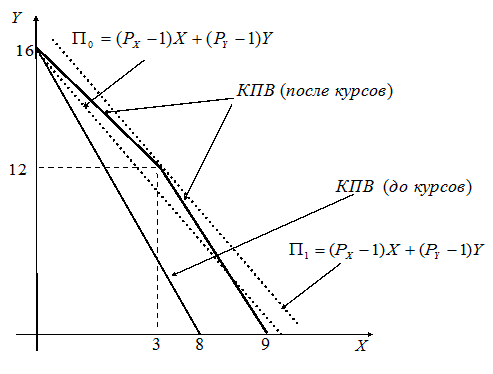
На рисунке ниже $П_{1}=69+10+6.$

Поскольку прибыль компании в этом случае меньше, чем до курсов повышения квалификации, то компания не станет проводить курсы повышения квалификации для своих сотрудников.

Графическое решение представлено на рисунке. Можно заметить, что построить КПВ после проведения курсов повышения квалификации можно и не описанным выше способом, а путем «сложения» двух КПВ, одна из которых – КПВ той части сотрудников, которая не повысила производительность после курсов, а другая – КПВ той части сотрудников, которая повысила производительность после курсов.

(в) Возможные ответы:
Сотрудники:

Сотрудники могут быть заинтересованы в курсах повышения квалификации. Расходы компании на оплату обучения сотрудников могут рассматриваться ими как субсидии на образование и порождать увеличение спроса на него. Например, в дальнейшем сотрудники могут менять место работы, а пройденные курсы могут свидетельствовать об их квалификации для будущих работодателей. Сотрудники могут сигнализировать о полезности будущих курсов, повышая производительность после уже пройденных курсов. Кроме того, если оплата труда работников зависит лишь от выполненного ими объема работы, некоторые сотрудники после повышения квалификации могут выполнять свою работу быстрее, высвобождая время для досуга, например.
Возможные концепции:

  • инвестиции в человеческий капитал
  • сигнализирование об уровне образования на рынке труда
  • максимизация удовлетворения (полезности) работника

Компании:
Не следует ожидать, что без материального стимулирования все сотрудники после прохождения курсов будут на деле демонстрировать повышение производительности. Поэтому повышение зарплаты сотрудников, прошедших обучение на курсах, компании могут не осуществлять. Однако, дополнительное образование сотрудников на курсах повышения квалификации может стимулировать часть сотрудников работать производительнее.

  • дифференциация работников на основе результатов КПК и поданных ими сигналов об изменении производительности может позволить в будущем пересмотреть ставки заработной платы сотрудников, что стимулирует их повысить свою производительность
  • курсы могут стимулировать конкуренцию между сотрудниками, что позволит компаниям находить среди своих сотрудников наиболее талантливых, работоспособных, что в будущем позволит отобрать наиболее производительных работников.
  • проведение курсов работники могут рассматривать как заботу фирмы о своих сотрудниках, что может также мотивировать их к повышению производительности и т.д.

Тем самым, компания может «находить» среди своих сотрудников активных, способных к обучению и повышению своей квалификации. Таким образом, компания может осуществлять отбор персонала, заинтересованного в качественной работе, что в дальнейшем может повысить доходы компании и компенсирует расходы на обучение сотрудников.
Кроме того, обучение сотрудников новым технологиям на курсах может снизить затраты компании в дальнейшем на переход к новым технологиям производства;
Основная концепция: анализ затрат-выгод.

2. Такси

Спрос на услуги маршрутных такси в городе N имеет вид $Q = 600 -p$, где $p$ — цена одной поездки в рублях, a $Q$ — количество поездок, которое горожане готовы приобрести по данной цене в течение недели. В городе N есть две фирмы, которые предоставляют услуги перевозок на маршрутных такси: «Автолайн» и «Минибус». Обе фирмы стремятся максимизировать свою прибыль. Общие издержки «Автолайна» описываются уравнением $TC_1 = 0{,}25q_1^2$, где $q_1$ — количество поездок, которое обеспечивают маршрутные такси фирмы «Автолайн» в течение недели. Функция общих издержек «Мииибуса» имеет вид $TC_2 = 0{,}5q_2^2$, где $q_2$ — количество поездок, которое обеспечивают маршрутные такси фирмы «Минибус» в течение недели.

В соответствии с местными законами, цену на услуги маршрутных такси в городе N устанавливает городская администрация (цена является единой для всех потребителей). Так сложилось, что глава этой администрации, Петр Петрович, является другом владельца фирмы «Автолайн» Ивана Ивановича. Поэтому Петр Петрович предложил Ивану Ивановичу выбрать цену на услуги маршрутных такси, которую в этом году установит администрация. Какую цену следует выбрать Ивану Ивановичу? 

Решение

Решение удобно начать с фирмы «Минибус», которая на цену никак влиять не может.
Функция прибыли «Минибуса» имеет вид: $p \times q_{2}−0,5q_{2}^{2}$. Это парабола с ветвями направленными вниз, и, следовательно, прибыль «Минибуса» максимальна при выпуске $q_{2}=p$.
Прибыль «Автолайна» равна $PR_{1}=p \times q_{1}−0,25q_{1}^{2}$, где цена на продукцию определяется владельцем автолайна и следующим образом связана с выпуском двух фирм: $p=600−q_{1}−q_{2}$.
Причём Иван Иванович знает, что $q_{2}=p$, поэтому понимает, что цена на продукцию его фирмы следующим образом связана с ее выпуском: $p=300−0,5q_{1}$. Подставляя последнее выражение в функцию прибыли «Автолайна», получаем: $$\begin{equation}PR_1=(300−0,5q_{1})\times q_{1}−0,25q_{1}^{2}\\ PR_{1}=300q_{1}−0,75q_{1}^{2}\end{equation}$$
Это парабола с ветвями направленными вниз, и, следовательно, прибыль «Автолайна» максимальна при выпуске $q_{1}=200$.
Следовательно, цена, которая обеспечит автолайну максимальную прибыль, равна $$p=300−0,5\times 200=200$$

3. Налоги

Государству необходимо соорать в казну 378 у.д.ед. Для достижения данной цели решено ввести потоварные налоги.
В отрасли, производящей товар X (ИКС), предельные издержки одной фирмы линейны, ценовая эластичность предложения одной фирмы равна единице при любом положительном выпуске. При этом равновесная цена на рынке товара X составляет 10 у.д.ед. Фирмы из отрасли X сырья не покупают, а их продукция потребляется исключительно отраслью Y (ИГРЕК).
Для производства любой одной единицы товара Y требуется одна единица товара X. Никаких иных затрат, кроме покупки X, фирмы из отрасли Y не несут. Функция спроса на продукцию Y имеет вид $Q_Y = 70 - P_Y$.
Число фирм при введении любого налога на рынке не меняется. Обе отрасли характеризуются условиями совершенной конкуренции. Потенциальные налогоплательщики не могут уйти от дополнительного налогового бремени.

(а) Найдите равновесные цены и выпуски в обеих отраслях до введения налогов.

(б) Среди экономистов разразилась дискуссия по поводу того, каким налогом облагать отрасли. Министр А — сторонник введения потоварного налога только на конечный продукт (Y). Он утверждает, что налог должны платить только производители Y по одинаковой ставке, установленной в у.д.ед. с каждой единицы товара.
Какую ставку налога следует установить в этом случае, чтобы собрать в казну требуемую сумму денег? Какими в этом случае будут равновесные выпуски и цены?

(в) Министр В настаивает на том, чтобы обе отрасли облагались потоварным налогом, но по разным ставкам, установленным в у.д.ед. с каждой единицы производимого товара.
Определите ставки налогов, предлагаемых министром В, равновесные выпуски и цены.

(г) Опираясь на результаты полученных расчетов, обоснуйте, сторону какого министра вы бы рекомендовали занять Правительству. Укажите, какими критериями вы руководствовались при поддержке позиции министра.

Решение

(а) На рынке совершенной конкуренции кривая индивидуального предложения совпадает с кривой предельных издержек выше минимума средних переменных затрат. Если издержки одной фирмы линейны, то можно записать $MC_{i}^{X}=bq_{i}^{X}+a$. Тогда, предложение одной фирмы тоже линейно. $MC_{i}^{X}=P_{X}$. Тот факт, что эластичность предложения одной фирмы равна $1$ при любом положительном выпуске, указывает на то, что $a=0$.
Так как для производства $1$ Y требуется $1$ X, то функция спроса на товар X будет эквивалентна функции спроса на товар Y: $Q_{X}=70-P_{X}$. Равновесная цена $X=10$ (по условию), значит, $Q_{X}^{*}=60$.

Рыночное предложение тоже является линейной функцией, выходящей из начала координат. По двум точкам $(0, 0)$ и $(60, 10)$ восстанавливаем функцию рыночного предложения Х: $Q_{S}^{X}=6P_{X}.$
Производственная функция $Q_{Y}=Q_{X}$
Общие издержки фирмы из отрасли Y: $TC_{Y}=P_{X} \times Q_{X}= P_{X} \times Q_{Y}$

На рынке $Y$ предельные затраты равны $MC_{i}^{Y}=P_{X}$. Условие максимизации прибыли: $MC_{i}=P$ следовательно, $P_{X}=P_{Y}$. Приравняв спрос и предложение на рынке $Y$, получим, что $P_{Y}^{*}=10, Q_{Y}^{*}=60.$

(б) Налог на отрасль $Y: P_{Y}^{D}=t_{Y}+P_{X}$, следовательно, $Q_{X}\equiv Q_{Y}$, тогда объёмы производства можно выразить через спрос на $Y$ и предложение $Х$. Получим уравнение: $$70-t_{Y}-P_{X}=6P_{X}, P_{X}=10-\dfrac{t_{Y}}{7}.$$ Выражаем объёмы производства через ставку налога: $Q_{Y}=60-\dfrac{6t_{y}}{7}$.

В казну необходимо собрать 378 у.д.ед. Получаем уравнение с единственной переменной:

$$Q_{Y}t_{Y}=(60-\dfrac{6t_{Y}}{7})t_{Y}=378$$

Решением уравнения являются 2 корня: $t_{Y}=7$ и $t_{Y}=63$

Параметры равновесия на обоих рынках:
$$t_{Y}=7 \Rightarrow Q_{Y}=Q_{X}=54, P_{Y}=16, P_{X}=9$$
$$ t_{Y}=63 \Rightarrow Q_{Y}=Q_{X}=6, P_{Y}=64, P_{X}=1$$

(в) Ставка налога на отрасль Х: $P_{X}^{D}=P_{X}^{S}+t_{X}$. Ставка налога на отрасль $Y: P_{Y}^{D}=P_{X}^{D}+t_{Y}=P_{Y}^{D}=P_{X}^{S}+t_{X}+t_{Y}$. Далее порядок действий совпадает с пунктом (б), что приводит к уравнению:
$$Q_{Y}t_{Y}+Q_{X}t_{X} = \left(60 - \dfrac{6}{7} (t_{X}+t_{Y}) \right) (t_{X}+t_{Y})=378$$

Решением уравнения являются 2 корня:$t_{Y}+t_{X}=7$ и $t_{Y}+t_{X}=63$

Ставки могут принимать любую неотрицательную величину, если выполняется одно из этих условий.

Параметры равновесия на обоих рынках:

$$ t_{X}+t_{Y}=7 \Rightarrow Q_{Y}=Q_{X}=54, P_{Y}=16, P_{X}= 9 + t_{X} (t_{X} \in [0, 7]) $$
$$ t_{X}+t_{Y}=63 \Rightarrow Q_{Y}=Q_{X}=6, P_{Y}=64, P_{X}= 1 + t_{X} (t_{X} \in [0, 63])$$

(г) Во-первых, политики должны выбрать меньшую ставку, потому что при ней чистые общественные потери меньше (если этого не сказано ранее).

Во-вторых, предложения министров А и В эквивалентны по всем критериям:

  • одинаковые налоговые сборы
  • одинаковые объёмы производства,
  • одинаковые цены конечного продукта
  • одинаковые потери общественного благосостояния

4. Слияния и поглощения

Во второй половине 1900-х годов стали популярными сделки по покупке одних компаний другими, называемые финансируемым выкупом (leveraged buy-out), или, сокращенно, LBO. Их суть такова: пусть X - относительно небольшая компания, стабильно приносящая доход, а А - компания, решившая купить X. При «обычной» сделке компания А оплатила бы за счет собственных средств 100% активов компании X. после чего сразу получила бы доступ к ее активам. В отличие от этой схемы, при LBO компания А оплачивает из собственных средств лишь незначительную долю от стоимости сделки (скажем, 20%), а оставшуюся часть (80% от стоимости сделки) оплачивает за счет взятого кредита в банке. При этом долговые обязательства по кредиту теперь будут числиться на счетах компании X. Эти обязательства будут погашаться в течение нескольких лет за счет прибыли, генерируемой компанией X. Так как прибыль компании X в результате выплаты долгов сократится, то X будет платить меньшую сумму в виде налога на прибыль. Эта разница по сравнению со случаем «обычной» сделки по приобретению X осядет в компании А, что делает такой вид сделок привлекательным для покупателей. После того, как долг будет полностью выплачен, контроль над компанией X перейдет к А.

(а) Опишите потенциальные риски инвесторов из компании А и банка-кредитора.

(б) Все крупнейшие за всю историю сделки LBO произошли в течение 20 лет между 1988 и 2007 годами. Почему после 2007 года не было крупных LBO?

Решение

Решение:

(а) Основные риски, возникающие в результате сделки LBO, связаны с большим долгом, за счет которого происходит покупка компании Х. Компания Х в результате шока или в силу каких-то других причин может перестать генерировать прибыль. В этом случае она не сможет расплатиться по долгам и будет объявлена банкротом. Тогда банк не сможет вернуть долг, а компания А лишится актива.

(б) Финансовый кризис, разразившийся в 2008 году, привел к пересмотру банками «безответственной» политики в отношении выдачи кредитов и, в итоге, к их удорожанию. Поскольку в процессе LBO большая часть покупки оплачивается на заемные средства, это сделало LBO существенно менее выгодными.

Есть и еще одна причина, тоже вызванная финансовым кризисом. Необходимым условием для успешного LBO является уверенность в том, что компания Х будет постоянно генерировать прибыль (в противном случае, X не сможет расплатиться по кредиту и обанкротится). Из-за турбулентности на финансовых рынках и проблем в экономике ряда ведущих стран степень уверенности в среднем стала существенно ниже.

Сделки LBO часто заключаются с целью перепродажи купленного актива по более высокой цене. В условиях падающих цен и кризиса продавцу сложнее рассчитывать на успех с поиском покупателя. Кроме того, в России наблюдается дефицит эффективных управленцев, способных увеличить стоимость вновь созданной компании и подготовить ее к продаже. В кризис это стало особенно очевидно. Слабая развитость фондового рынка также усложняет выход из актива.

5. Два завода

Фирма Ивана Ивановича продает сахар на рынке совершенной конкуренции. Фирма может производить сахар на двух заводах. При этом функция издержек на первом заводе имеет вид:
$$
TC_1=\begin{cases}
q_1^2+q_1+100, &\text{ если } q_1>0,\\
0, &\text{ если } q_1=0,
\end{cases}
$$
а на втором заводе:
$$
TC_2=\begin{cases}
2q_2^2+q_2+28, &\text{ если } q_2>0,\\
0, &\text{ если } q_2=0.
\end{cases}
$$

(а) Предположим, что Иван Иванович не может производить сахар сразу на двух заводах. Какой из заводов он выберет при различных уровнях цен? Определите аналитически и проиллюстрируйте графически предложение фирмы. Считайте, что объем выпуска может быть любым вещественным числом.

(б) Пусть Иван Иванович может производить продукт на двух заводах. Как изменится функция предложения фирмы? Приведите графическую иллюстрацию. Сколько сахара будет производиться на каждом из заводов?

(в) Предположим, что Иван Иванович является монополистом на рынке сахара, а функция спроса на сахар имеет вид $q=37-p$, где $q = q_1+q_2$ (Иван Иванович может производить сахар на двух заводах). Какое количество сахара будет произведено, и по какой цене он будет продан?

Решение

(а) Выведем оптимальное правило производства на каждом из заводов, если выбрать этот завод. Если использовать первый завод, то функция прибыли Ивана Ивановича будет иметь вид

$$pq_{1}-q_{1}^{2}-q_{1}-100.$$

Найдём максимум этой функции.
$$p-1-2q_{1}=0 \phantom $(-2<0 \Rightarrow max) $$
$$q_{1}=\dfrac{p-1}{2}$$

В этом случае прибыль Ивана Ивановича будет равна

$$\dfrac{(p-1)^{2}}{4}-100.$$

Теперь рассмотрим прибыль Ивана Ивановича, если он будет производить на втором заводе. Функция прибыли будет иметь вид

$$pq_{2}-2q_{2}^{2}-q_{2}-28.$$

Найдём максимум этой функции.

$$p-1-4q_{2}=0 \phantom $(-4<0 \Rightarrow max) $$
$$q_{1}= \dfrac{p-1}{4}$$

В этом случае прибыль Ивана Ивановича будет равна
$$\dfrac{(p-1)^{2}}{8}-28.$$

Сравним теперь, при каких ценах прибыль на каком заводе выше.
\begin{align}
\dfrac{(p-1)^{2}}{4} - 100 \quad &vs. \quad \dfrac{(p-1)^2}{8}-28\\
\dfrac{(p-1)^2}{8}\quad &vs.\quad 72\\
(p-1)^2 \quad &vs. \quad 8^{2}\cdot 3^{2}\\
p-1 \quad &vs.\quad 24\\
p\quad &vs. \quad 25\\
\end{align}

Итак, если цена выше 25, то лучше производить (если вообще производить) на первом заводе. Если же цена меньше 25, то на втором. Теперь нужно найти, при какой цене вообще выгодно производить сахар. Видим, что при цене 25 прибыль Ивана Ивановича положительна. Тогда, чтобы найти минимальную цену, при которой выгодно производить, сравним прибыль от производства на втором заводе с нулём.
\begin{align}
\dfrac{(p-1)^{2}}{8}-28 \quad &vs.\quad 0\\
(p-1)^{2}\quad &vs.\quad 14\cdot 4^{2}\\
p-1\quad &vs.\quad 4\sqrt{14}\\
p\quad &vs.\quad 4\sqrt{14}+1<25\\
\end{align}
Итак, вообще выгодно производить при цене выше $4\sqrt{14}+1$. Тогда получаем следующее предложение фирмы Ивана Ивановича.

\begin{equation}
q=
\left\{
\begin{aligned}
0\quad&, p < 4\sqrt{14}+1\\
\dfrac{p-1}{4}&, p \in [4\sqrt{14}+1; 25]\\
\dfrac{p-1}{2}&, p>25\\
\end{aligned}
\right.
\end{equation}

Остаётся нарисовать график предложения.

(б) Так как производство на одном заводе не влияет на производство на другом заводе, то нам достаточно понять, когда производство на каждом из заводов в отдельности прибыльно. Для второго завода мы уже это нашли в первом пункте. Найдём это для первого завода.

\begin{align}
\dfrac{(p-1)^{2}}{4}-100 \quad &vs.\quad 0\\
p-1 \quad &vs. \quad 20\\
p \quad &vs. \quad 21\\
\end{align}

Итак, на первом заводе прибыльно производить при цене больше 21. Тогда, начиная от этой цены, Иван Иванович будет использовать сразу оба завода. Сложив кривые предложения двух заводов, мы получаем, что общее предложение при цене больше 21 будет иметь вид

$$q=\dfrac{3(p-1)}{4}.$$
Тогда общая кривая предложения будет иметь вид

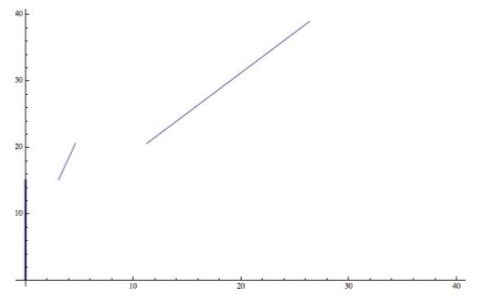
\begin{equation}
q=
\left\{
\begin{aligned}
0\qquad&, p < 4\sqrt{14}+1\\
\dfrac{p-1}{4}\quad&, p \in [4\sqrt{14}+1; 21]\\
\dfrac{3(p-1)}{4}&, p>21\\
\end{aligned}
\right.
\end{equation}

Остаётся нарисовать график предложения.

(в) Для Ивана Ивановича существует 4 варианта производства: не производить вообще, производить на первом заводе, производить на втором заводе и производить на обоих заводах сразу. Чтобы понять какой из вариантов предпочтительнее, решим отдельно задачу максимизации прибыли в каждом из четырех случаев. Если не производить вообще, прибыль равна 0.
Если используется только первый завод, то из условия $MR=MC$ находим, что
$2q+1=37-2q$ и оптимальным выпуском будет $q=9$, а прибыль будет равна
$$(37-9)\cdot 9 -81 - 9- 100 =62.$$
Если используется только второй завод, то из условия $MR=MC$ находим, что $4q+1=37-2q$и оптимальным выпуском будет $q=6$. Тогда его прибыль будет равна
$$(37-6)\cdot 6 -2\cdot 36 - 6- 28 =80.$$
(+3 балла) Если используются оба завода, то необходимо найти, в какой пропорции они будут использоваться. При фиксированном суммарном выпуске $q=q_{1}+q_{2}$ предельные издержки производства на каждом из двух заводов должны быть равны, откуда получаем $2q_{1}+1=4q_{2}+1$. Поэтому

$$q_{1}=\dfrac{2q}{3}, \quad q_{2}=\dfrac{q}{3}.$$
Тогда общие издержки равны
$$TC(q)=\dfrac{2q^{2}}{3}+q+128$$
Максимизируя прибыль, из условия $MR=MC$, получаем $q=10.8$, а соответствующая прибыль будет равна
$$(37-10.8)\cdot10.8 - \dfrac{2\cdot10.8^2}{3} - 10.8 - 128 =$$
$$= (37-19)\cdot 10.8-128=66.4.$$
Итак, видим, что прибыль будет наибольшей, если $q=6$. Это и будет количество сахара, которое продаст Иван Иванович. Цена на сахар в этом случае будет
$$37-6=31.$$

6. Экономисты-неудачники

(а) Юный экономист Митрофан П. анализировал отдачу от инвестиций в образование — прирост доходов после окончания университета. Он выяснил, что обладатели диплома Престижных университетов зарабатывают заметно больше своих сверстников. Однако обнаружились интересные детали. Люди, поступившие в Престижный университет, но по каким-то причинам выбравшие учебу в одном из Скромных университетов, зарабатывали не меньше, чем выпускники Престижных. Более того, среди выпускников Скромных университетов зарабатывали больше те, кто подавал свои документы в Престижные, даже если их не приняли в последние. Узнав об этом, Митрофан П. с целью увеличения будущих заработков отправил документы в Престижный университет — несмотря на то, что учиться в нем не планировал.
Вопреки ожиданиям, он потом получал такие же доходы, как средний выпускник Скромных университетов.

(б) Молодой экономист Остап Б. решил создать стартап. Он разработал проект «iЯма». Проект предполагал разработку за счет городского бюджета специального приложения для смартфонов, который, находясь в автомобиле, с помощью встроенного акселерометра будет автоматически отсылать в городские дорожные службы GPS-данные о встреченных на дороге ямах, провалах и крупных трещинах в покрытии. Остап Б. утверждал, что эта разработка существенно сократит издержки на мониторинг покрытия и улучшит качество дорог во всем городе.
Вопреки ожиданиям, после открытия продаж этого приложения, дорожные службы стали чаще чинить дороги, которые находились в самом хорошем состоянии, и реже — самые проблемные участки дорог.

(в) Известный экономист Павел Иванович Ч., уволенный из университета, устроился на работу в правительство, в котором курировал вопросы социальной политики. В частности, он выяснил, что почти все молодые люди, состоящие на учете в полиции, регулярно смотрят криминальные боевики в кинотеатрах. С целью снижения преступности с участием подростков и молодежи он разработал законопроект о существенном повышении возрастного ценза на соответствующие картины.
Вопреки ожиданиям, преступность после этого не сократилась, а кое-где даже выросла.

Во всех случаях действия экономистов не привели к ожидаемому результату. Объясните, для трех случаев - почему.

Решение

(a) Ошибка экономиста заключается в том, что он принимает сигнал о индивидуальных качествах за причину высоких заработков. Из эмпирических фактов, приведенных в условии, следует, что выпускники престижных университетов зарабатывают больше, чем выпускники скромных, не из-за качества образования, а из-за отбора на входе. Другими словами, изначальные характеристики абитуриента важнее, чем знания и навыки, полученные в университете. Однако помимо объективных способностей, тестируемых на входе в университет, значение может иметь субъективная оценка собственных способностей, амбиции, самоуверенность. Эти качества, которые впоследствии помогают добиваться относительно более высоких заработков, отражаются подачей документов в престижный университет.

(б) Стартап, очевидно, столкнулся со смещением выборки маршрутов, по которым ездили автомобили, посылавшие сигналы в городские службы. Во-первых, это смещение на уровне покупки – приложения устанавливали только те, у кого был автомобиль и смартфон и готовность тратить собственные средства на решение общественных проблем.Скорее всего, эти люди жили и работали в хороших районах с хорошими дорогами. Во-вторых, это смещение на уровне выбора маршрута: водители будут пытаться избегать наиболее проблемных участков.

(в) Экономист совершил неправильный вывод о причинно-следственной связи на основе имевшихся у него данных. Не молодые люди становились преступниками из-за просмотра криминальных боевиков, а смотрели криминальные боевики, поскольку обладали склонностью к преступному поведению. Поэтому повышение ценза не вызвало ожидаемого падения преступности. Если же предположить, что просмотр фильмов определенного содержания и личное девиантное поведение до определенной степени являются субститутами – то неудивительно, что преступность могла даже возрастать.

2-й тур: Задачи

1. Учитель и ученики

Рассмотрим модель взаимодействия учителя и учеников в обычном классе средней общеобразовательной школы. Для учеников пусть существуют следующие характеристики: усилия $e_s$ и результаты $r_s=e_s-\frac{e_s^2}{e_t}$ (успеваемость); для учителя: зарплата $w$, усилия $e_t$ и полезность $U_t=w\cdot r_s-e_t^2$. Зарплата является экзогенной величиной, которую устанавливает администрация школы. Каждый из агентов выбирает свой уровень усилий, максимизируя при этом либо результат (ученики), либо полезность (учитель).
Порядок действий следующий:

  • администрацией назначается некий уровень зарплаты для учителя;
  • учитель выбирает уровень усилий;
  • ученики выбирают уровень усилий.

Учитель и ученики знакомы давно, а потому знают, какую целевую функцию максимизирует каждый из них.

(а) Найдите равновесные уровни усилий для учителя и учеников.

(б) Пусть теперь администрация выбирает уровень зарплаты учителя, исходя из максимизации собственной полезности $U_a=r_s+U_t-w^2/32$ . Чему равны равновесные уровни зарплаты и усилий?

(в) Вернемся снова к первому пункту. Пусть теперь учителя вообще не интересуют результаты учеников: $U_t=w/64-e_t^2$, однако, если учитель будет прикладывать усилия меньше чем 1/16, то его уволят, и он не будет получать зарплату. Найдите равновесные уровни усилий и результаты учеников в данном случае. Определите, при каком уровне зарплаты учителю все равно, учитывать или нет результаты учеников.

Решение

(а) Согласно заданному порядку действий верна обратная индукция: сначала ученики определяют оптимальный уровень своих усилий, максимизируя свои результаты при заданном уровне усилий учителя:
$$r_{s}=e_{s}-\dfrac{e_{s}^{2}}{e_{t}}\to max$$
Функция результатов является квадратной с ветвями вниз относительно усилий учеников, следовательно, ее максимум находится в вершине:
$$\begin{equation}e_{s}=\frac{e_{t}}{2}\\
r_{s}=\dfrac{e_{t}}{4}\end{equation}$$

Теперь учитель максимизирует свою полезность, зная уровень усилий учеников и при заданной экзогенно зарплате:

$$U_{t}=w\cdot r_{s}-e_{t}^{2}=U_{t}=w\cdot \dfrac{e_{t}}{4}-e_{t}^{2} \to max$$
Функция полезности учителя является квадратной с ветвями вниз относительно усилий учителя, следовательно, ее максимум находится в вершине:
$$\begin{equation}e_{t}=w/8 \\
\text{Тогда } e_{s}=\dfrac{e_{t}}{2}=\dfrac{w}{16}; r_{s}=\dfrac{e_{t}}{4}=\dfrac{w}{32}; U_{t}=\dfrac{w^{2}}{64} \end{equation}$$

(б) Поскольку учитель считает уровень зарплаты заданным, то новое условие – последний шаг в обратной индукции: теперь администрация максимизирует свою полезность, зная, какие уровни усилий будут выбирать учитель и ученики:
$$U_{a}=r_{s}+U_{t}-\dfrac{w^{2}}{32}=\dfrac{w}{32}+\dfrac{w^{2}}{64}-\dfrac{w^{2}}{32}=\dfrac{w}{32}-\dfrac{w^{2}}{64} \to max$$
Функция полезности администрации является параболой с ветвями вниз относительно зарплаты, следовательно, ее максимум находится в вершине:
$$\begin{equation}w=1\\
\text{Тогда } e_{t}=w/8=\dfrac{1}{8}; e_{s}=\dfrac{e_{t}}{2}=\dfrac{w}{16}=\dfrac{1}{16}\end{equation}$$

(в) Так как учитель не хочет быть уволенным и не получать зарплату (его полезность тогда будет равна 0), то он будет прикладывать усилия больше либо равные 1/16. Так как в функции полезности его усилия входят в виде $(-e^{2}_{t})$, то ему нет смысла выбирать уровень усилий больший 1/16. Следовательно, учитель будет выбирать $e_{t}=\dfrac{1}{16}.$ Тогда $e_{s}=\dfrac{1}{32}.$ Максимум полезности в этом случае равен $U_{t}=\dfrac{w}{64}-\dfrac{1}{256}$.
Найдем, при каком уровне зарплаты учителю будет все равно:
$$\begin{equation}\dfrac{w}{64}-\dfrac{1}{256}=\dfrac{w^{2}}{64}\\
w=\dfrac{1}{2}\end{equation}$$

2. Война?!

В королевстве еды и вина правит доблестный король Ешьдапей. Жители королевства умеют производить только еду и вино. При этом за один человеко-час можно произвести либо одну единицу еды, либо половину единицы вина. Также можно производить любую допустимую комбинацию двух товаров, учитывая то, что альтернативные издержки производства каждого из товаров постоянны. Всего в распоряжении короля имеется 10 человеко-часов ежедневно. Ешьдапей размышляет над тем, следует ли ему вступать в войну с очень большим соседним королевством вина и еды. Чтобы завоевать $H$ земель соседнего королевства, Ешьдапею нужно навсегда потерять $H$ из 10 человеко-часов, которыми он располагает ежедневно. При этом $H$ завоёванных территорий приносят королю $H$ новых человеко-часов ежедневно. Единственная разница между этими новыми
жителями и жителями королевства еды и вина заключается в том, что за один человеко-час новые жители умеют произвести либо не более одной единицы вина, либо не более половины единицы еды. Заметим, что Ешьдапей может указывать своим подданным, как им распределять свои силы между производством вина и еды.

(а) Ешьдапей непременно хочет, чтобы еды и вина производилось равное количество и чем больше, тем лучше. Сколько земель тогда решит завоевать правитель королевства еды и вина? Приведите графическую иллюстрацию.
(б) Как изменится решение короля, если ради завоевания $H$ новых земель, ему теперь придется навсегда потерять $2H$ из 10 своих человеко-часов? Приведите графическую иллюстрацию.
(в) Теперь ради завоевания $H$ новых земель, Ешьдапею придется навсегда потерять $H^2$ своих человеко-часов. Сколько новых земель решит завоевать король?

Решение

(а) При отсутствии войны король Ешьдапей может добиться $B=E=\dfrac{10}{3}$.

При войне общее количество часов не меняется.

Заметим, что жители королевства еды и вина умеют лучше производить еду, а жители королевства вина и еды умеют лучше производить вино. Следовательно, так как Ешьдапей имеет возможность «обменять» $H$ своих человеко-часов на $H$ человеко-часов соседнего королевства, то ему имеет смысл «обменять» их так, чтобы всю еду производили на его изначальной территории, а чтобы всё вино производили на завоёванной территории. Другими словами, точка перелома новой КПВ должна находиться на прямой $y=x$, где $y$ обозначает количество еды, а $x$ — количество вина. В то же время в точке перелома $x=H$, а $y=10-H.$ Следовательно, оптимальным $H$ будет тогда, когда будет выполняться следующее равенство.
$$H=10-H.$$
$$H=5.$$

Если $H=5$, то можно обеспечить $B=E=5>10/3$, если $H\ne5$, то из условия $B=E$ следует, что кто-то работает не по специальности. Поэтому $B=E<5$.

Приведем теперь графическую иллюстрацию.

(б) Теперь король может «обменять» $2H$ из своих человеко-часов на $H$ человеко-часов соседнего государства. Можно заметить, что Король не сможет обеспечить лучший выбор в результате ни от одного из обменов.

Н приобретенных иностранцев смогут произвести $E=H$ или $B=0,5H$.

2Н потерянных соотечественников могли произвести $E=2H$ или $B=H$.

Но при каких-то войнах ему может быть не хуже, чем раньше. А именно, при таких войнах, что он сможет получить $B=E=\dfrac{10}{3}$ .
А это, в свою очередь, выполняется при $H\le \dfrac{10}{3}$ (то есть пока новых иностранцев не придется задействовать не по их специализации).

Ответ: $H\in[0;10/3]$

Приведем теперь графическую иллюстрацию.

(в) Если $H>2$, то решение аналогично решению п. (б), король точно не будет воевать. Пусть далее $H\le2$. Первоначально $10/3$ работали на производстве $E$, $20/3$ работали на производстве $B$. Зафиксируем $E$. Если захватим $H$ земель, то потеряем в вине $ \dfrac{H^{2}}{2}$, а приобретем $H$.

Максимизируем $-\dfrac{H^{2}}{2}+H$, получаем $H=1$. Таким образом, среди $H\in[0,2]$ оптимальным вариантом является $H=1$.

3. Дороги и ...

В королевстве Озерном есть пять городов: A, B, C, D, E. Они расположены в указанной последовательности вокруг большого озера. Расстояние от города А до города B составляет 4 км, от В до С — 13 км, от С до D — 6 км, от D до E — 12 км, наконец, от E до A — 11 км. Дорога вокруг озера, которая соединяет города, находится в ужасном состоянии. Парламент Озерного королевства хотел бы, чтобы была построена новая асфальтовая дорога. Для этого он нанимает строительную компанию «Дорстрой».

Парламент расположен в городе А (столице) и готов выплатить «Дорстрою» $P$ золотых монет за каждый город, из которого можно будет доехать до столицы по асфальтовой дороге (величина $P$ одинакова для каждого города, независимо от расстояния между ним и столицей).

Строительство каждого километра дороги обходится «Дорстрою» в 100 золотых монет, и руководство этой фирмы стремится максимизировать свою прибыль.

(а) Для каждого значения $P$ укажите, какие города будут соединены со столицей асфальтовой дорогой. (Для тех случаев, когда «Дорстрою» одинаково выгодны несколько вариантов длины дороги, считайте, что «Дорстрой» всегда выбирает самый длинный.)

(б) Для каждого значения $P$ укажите максимальную прибыль фирмы «Дорстрой».

Решение

Построим функцию издержек фирмы «Дорстрой».

Ясно, что если «Дорстрой» решит соединить со столицей только один город, то это будет город $B$, так как до него от столицы ближе всего.

Если же фирма решит присоединить к столице два города, то это буду города $B$ и $E$, так как в этом случае длина дороги составит $11+4=15$ километров. Во всех других случаях требуемая длина дороги будет больше: если соединять со столицей города $B$ и $C$, то придется построить $4+13=17$ километров дороги; а если города $E$ и $D$, то и того больше $(11+12=33).$

Аналогично, легко проверить, что если «Дорстрой» примет решение соединить со столицей три города, то это будут города $B$, $C$, $D$. И длина дороги составит $4+13+6=23$ километра.

Наконец, если соединять со столицей все четыре города, то следует протянуть дорогу $C$-$D$-$E$-$A$-$B$, и в этом случае ее длина будет равна $6+12+11+4=33$ километра.

Занесем эти данные в таблицу, рассчитав общие и предельные издержки строительной компании.

Количество
городов,
соединенных
асфальтовой дорогой со
столицей (выпуск фирмы)		 Список городов
(черточки обозначают
соединение городов
дорогой)		 Длина дороги Общие издержки Предельные издержки
1 A-B 4 400 400
2 E-A-B 15 1500 1100
3 A-B-C-D 23 2300 800
4 C-D-E-A-B 33 3300 1000

Фирма «Дорстрой» является ценополучателем, поэтому для нее определена функция предложения. Определив предельные издержки «Дорстроя» мы можем любым из стандартных способов определить его функцию предложения:

$p\in [0,400]$ $q=0$: ни один город не соединен со столицей асфальтовой дорогой.
$p\in [400,950]$ $q=1:$ город B соединен асфальтовой дорогой со столицей.
$p\in [950,1000]$ $q=3$: города $B$,$ C$,$ D$ соединены асфальтовой дорогой со столицей.
$p>1000$ $q=4$: все города соединены дорогой со столицей

Наконец, зная функцию предложения, мы можем определить максимальную прибыль фирмы.

$p\in [0,400]$ Прибыль$\text{ } =0$
$p\in [400,950]$ Прибыль$\text{ } =P-400$
$p\in [950,1000]$ Прибыль$\text{ }=3P-2300$
$p>1000$ Прибыль$\text{ }=4P-3300$

4. Ожидания

В закрытой экономике страны Альфа продается единственный конечный товар, который производят 100 одинаковых фирм. Выпуск каждой из фирм ($y$) следующим образом зависит от количества используемых ею работников ($L$): $y=2\sqrt{L}$. Заработная плата одного работника устанавливается профсоюзом и составляет 2 денежные единицы (д.ед.), фирмы никак не могут на нее влиять. Совокупный спрос в рассматриваемой экономике описывается уравнением:
$$
Y=40+1{,}2\frac{M}{P},
$$
где $Y$ — величина совокупного спроса, $M$ —денежная масса (д.ед.), $P$ — уровень цен.

(а) Известно, что денежная масса в стране Альфа составляет 50 д.ед., и экономика этой страны находится в состоянии краткосрочного равновесия. Определите равновесные уровни цен и выпуска в этой стране.

(б) Центральный банк страны Альфа решил стимулировать экономику путем неожиданного увеличения денежной массы на 60 %. На сколько процентов в результате этого события изменятся уровень цен и выпуск?

(в) Предположим, что профсоюз страны Альфа прознал о планах центрального банка. Поэтому лидеры профсоюза решили пересмотреть устанавливаемую ими номинальную зарплату таким образом, чтобы реальная заработная плата каждого работника осталась такой же, как в пункте (а). Какую номинальную зарплату установят лидеры профсоюза? На сколько процентов в результате указанных событий (изменения денежной массы и изменения номинальной заработной платы) увеличатся уровни цен и выпуска в экономике страны Альфа?

(г) Сопоставив результаты пунктов (б) и (в), сделайте вывод о том, какая стимулирующая политика является более эффективной: неожиданная или ожидаемая? (Этот пункт оценивается только в случае получения верных ответов на вопросы пунктов (а)-(в))

Решение

(а) Задача максимизации прибыли фирмы: $PR=P\cdot 2\sqrt{L}-wL.$

Решая эту задачу, получаем функцию спроса каждой фирмы на труд: $L=\left(\dfrac{p}{2}\right)^{2}$. Подставляя это условие в производственную функцию, получаем предложение одной фирмы: $y=2\dfrac{p}{w}=p$. Следовательно, совокупное предложение имеет вид: $Y=100P.$

Из равенства совокупного спроса и совокупного предложения находим, что $P=1, Y=100.$

(б) Новая функция спроса имеет вид: $Y=40+1{,}2\cdot \dfrac {50\cdot 1{,}6}{p}.$ Из равенства нового совокупного спроса и прежнего совокупного предложения находим, что $P=1{,}2, Y=120.$ Таким образом, и уровень цен, и выпуск выросли на $20\%.$

(в) В пункте (а) реальная заработная плата была равна $2$. Отметим (см. формулу в пункте (а)), что величина спроса фирмы на труд, а, следовательно, и величина ее предложения однозначно определяются реальной заработной платой. Таким образом, если реальная заработная плата не изменилась по сравнению с пунктом (а), то и выпуск каждой фирмы не изменился по сравнению с пунктом (а), а следовательно совокупный выпуск будет по-прежнему равен $100$. Подставив этот результат в функцию совокупного спроса, находим новый уровень цен, который равен $1{,}6$. Выпуск вырастет на $0\%$. Уровень цен вырастет на $60\%$. Новая номинальная заработная плата будет равна $2\cdot1{,}6=3{,}2$.

(г) В пункте (б) выпуск вырос, а в пункте (в) остался без изменений, следовательно неожиданная политика более эффективна для стимулирующего выпуска, чем ожидаемая.

5. Государственный долг

Сильвия Назар в книге «Путь к великой цели» описала экономические и финансовые трудности, с которыми столкнулась в 1919 году послевоенная Австрийская республика. Одной из основных трудностей был огромный долг, за счет которого финансировалось ведение военных действий в Первой мировой войне.

(а) «Историк Ниал Фергюсон писал, что существует пять и только пять способов облегчить такое бремя <военного долга>: это официальный (де-юре) отказ от выплат,…, различные варианты отказа де-факто… Наконец, самый достойный вариант – это просто расплатиться по долгам».
Приведите аргументы в пользу того, почему оплата долгов может быть лучше для экономики, чем отказ от обязательств?

(б) Предположим, что официальный отказ от выплаты долга больше не рассматривается. Опишите три различных возможных способа погашения военного долга (более трех способов приводить не стоит – в этом случае будут рассмотрены только первые три).

(в) «Шумпетер <министр финансов Австрийской республики> предпочел иное решение заставить богатых оплатить военный долг Австрии, взяв с них высокий одноразовый налог на имущество».
Чем одноразовый налог на имущество богатых может быть лучше, чем увеличение
подоходного налога для той же группы населения?

(г) «Шумпетер не пробыл в должности министра финансов и трех дней, как крона начала свободное падение».
Почему объявление о планах по введению единоразового налога на имущество могло вызвать падение национальной валюты?

Решение

а) Отказ от оплаты долгов вызовет полную утрату доверия со стороны инвесторов. Восстановление репутации правительства как надежного партнера займет продолжительное время, а недополученные в результате этого инвестиции могут обернуться большими потерями для экономики, чем изначальная сумма долга.

Возможные варианты ответов:

  • Потеря доверия приводит к невозможности получения кредита в будущем
  • Сохранение доверия приводит к сохранению инвестиций, что позволяет развиваться в будущем
  • Падает политический вес государства
  • Возможны ответные санкции
  • Дефолт, уменьшение богатства, снижение потребления, сокращение совокупного спроса, падение ВВП
  • Социальная напряженность в обществе

б) Во-первых, можно выпустить государственные облигации и постараться привлечь тем самым средства внешних заемщиков. Во-вторых, можно включить печатный станок и собрать инфляционный налог со всех держателей национальной валюты. В-третьих, можно попробовать продать государственную собственность.

Возможные варианты ответов:

  • Внутренний и внешний займы
  • Эмиссия денежных средств
  • Меры сдерживающей фискальной политики
  • Продажа (аренда) территорий
  • Продажа золотовалютных резервов
  • Продажа государственной собственности

в) Одноразовый налог, будучи выплачен один раз, создает меньше отрицательных стимулов для инвестиций в экономику страны со стороны богатого населения в будущем, чем увеличение налога на доходы.

Единоразовый налог на имущество в меньшей степени меняет поведение, а подоходный вызывает стимулы к уклонению от уплаты налогов, снижение стимулов к работе.

Подоходный подрывает стимулы к экономической активности, в результате чего создаются предпосылки для сокращения ВВП и налоговых сборов. Налог на имущество легче собирается – сложно скрыть имущество.

г) В результате объявления о грядущем единоразовом налоге неизбежно начнется вывод средств за пределы Австрийской республики. Он будет сопряжен с покупкой иностранной валюты и продажей австрийской кроны, что и приведет к падению курса.

Логическая цепочка: отток капитала за рубеж, рост предложения кроны и рост спроса на иностранную валюту, в результате – падение валютного курса кроны.

6. Бесплатные услуги

(а) Некоторые работодатели предоставляют своим работникам определенный набор компенсаций и льгот социального характера, который не предусмотрен трудовым кодексом и иными нормативными актами, так называемый «социальный пакет». Предоставление работодателем социального пакета не является его обязанностью и зависит исключительно от желания самого работодателя и его финансовых возможностей. В частности, в подобный пакет может входить бесплатное для сотрудника медицинское страхование, оплата проезда работников. Работодатель в этом случае несет значительные затраты по страхованию своих сотрудников или оплате транспортных расходов. Почему руководство компаний предпочитает самостоятельно приобретать страховые полисы для нанятых людей и/или оплачивать или организовывать их проезд от места жительства до места работы и обратно, в то время как многие работники предпочли бы увеличение годовой заработной платы на сумму, равную годовым расходам компании на каждого сотрудника?

(б) Некоторые экономисты утверждают, что если сделать общественный транспорт города полностью бесплатным, то это принесет бюджету города огромную экономию. В некоторых городах мира общественный транспорт (или какая-то его часть) совершенно бесплатен для пассажиров. Опишите выгоды, которые может получить город от такой политики. Объясните также, почему не все города мира переходят на подобную политику ценообразования на услуги общественного транспорта.

Решение

(а) Соцпакеты:

  1. Асимметрия информации. У работодателя нет гарантий, что сотрудники будут приобретать медицинский полис самостоятельно или ответственно заботиться о своем здоровье.
  2. Наличие медицинского полиса (пусть даже и бесплатного) может стимулировать сотрудников своевременно обращаться к врачам, что снизит впоследствии издержки работодателя на поиск замены сотрудника и связанные с ней дополнительные расходы во время его нетрудоспособности.
  3. Наличие в социальном пакете сотрудника медицинского страхования и/или оплата его проезда на транспорте может являться хорошим материальным стимулом для сотрудников и удерживать от смены места работы хороших опытных специалистов.
  4. Организация проезда сотрудников до места работы позволяет дисциплинировать работников и обеспечивает их своевременную доставку к рабочему месту, вследствие чего работодатель может сократить свои расходы, связанные с опозданием сотрудников и несвоевременным выполнением ими своих обязанностей.

(б) Транспорт:
Выгода:

  1. Большое количество людей захотят пересесть с личных автомобилей на общественный транспорт, что сократит количество частных автомобилей на дорогах. Это, в свою очередь, снизит уровень загрязнения в городе, количество пробок на дорогах, что, кроме всего прочего, обеспечит бесперебойную работу различных городских служб.
  2. Сократятся расходы города, в котором общественный транспорт контролируется и обслуживается за счет муниципальной казны, на контроль оплаты проезда, установку и обслуживание турникетов, выпуск проездных билетов, оплату труда кассиров.
  3. Повышение роли более экологичного транспорта (трамваи, троллейбусы, метро) снизит объем потребления нефтепродуктов, что также снизит уровень загрязнения окружающей среды.
  4. Сократит расходы муниципальных властей на оплату работы чиновников, которые курируют различные транспортные льготы.

Причины, по которым не все города переходят на бесплатный общественный транспорт:

  1. Для того, чтобы стимулировать людей пересесть на общественный транспорт с личного, необходимо, чтобы сеть общественного транспорта была хорошо развита, а маршруты хорошо продуманы и организованы. Это может требовать значительных затрат муниципалитета.
  2. При наличии платы за проезд, оплата городского транспорта финансируется за счет муниципальной казны (собранные налоги) и самими пассажирами. Отмена оплаты за проезд может приводить к увеличению муниципальных расходов, и как следствие, повышение уровня некоторых налогов, что может вызвать неодобрение жителей города.
  3. При значительном социальном расслоении часть граждан может проявлять негодование по поводу того, что они вынуждены оплачивать проезд остальных жителей, в то время как сами они не пользуются общественным транспортом.
  4. В больших городах большую роль играет коммерческий общественный транспорт. Введение бесплатного проезда может повысить конкуренцию между транспортными компаниями, что может значительно снизить их прибыль, или побудить некоторые частные транспортные компании прекратить свою деятельность. Заинтересованность в коммерческих транспортных компаниях большого количества чиновников может служить дополнительными препятствиями в переходе на бесплатный общественный транспорт.