1. Задача Считалкина
Условие. Выручка авиастроительной фирмы задается уравнением $TR = 12Q - 0{,}9Q^2$, где $Q$ — количество самолетов (в штуках), продаваемых в месяц. Функция общих затрат этой фирмы задается уравнением $TC = 12 + 2Q - 0{,}7Q^2 + 0{,}03Q^3$. Найдите, при каком $Q$ фирма получит максимально возможную выручку, и при каком $Q$ фирма получит максимальную прибыль.
Решение. Максимальную выручку можно найти из равенства нулю производной: $TR'= 12 - 1{,}8Q = 0$, то есть $Q = 6{,}(6)$. Максимальная прибыль определяется из условия $MR = MC$, где $MR = TR' = 12 - 1{,}8Q$, а $MC = TC' = 2 - 1{,}4Q +0{,}09 Q^2$, т. е. $12 - 1{,}8Q = 2 - 1{,}4Q +0{,}09 Q^2$. Решаем полученное квадратное уравнение, находим, что оно имеет два корня, $Q = 8{,}55$ и $Q = -12{,}955$. Из двух коней берем неотрицательный, и получаем, что максимальную прибыль фирма получит при $Q = 8{,}55$.
Филу задача казалась замечательной, но К. П. Вешкин не разделил его энтузиазма и сказал: «Дорогой Фил, вы, как будущий экономист, должны хорошо владеть математикой. Однако хороший экономист — это больше, чем только математик. Посему за ваше домашнее задание я вам ставлю по математике „пять“, а по экономике „два“». Объясните, что в задаче Фила не понравилось вредному учителю? Приведите как минимум три критических замечания. Из них хотя бы два должны достаточно серьезны, чтобы объяснить, почему К. П. Вешкин влепил бедному Филу «два» по экономике.
1. Исходя из здравого смысла количество самолетов определено только на множестве целых чисел, так что использование непрерывных функций, производных, и, особенно дробных ответов не имеет экономического смысла (самое очевидное и наименее серьезное)
2. Объем выпуска $Q_2$ лежит на убывающей части кривой $TC$ (которая, исходя их экономического смысла, обычно считается строго возрастающей). Поэтому $Q_2$ получилось больше $Q_1$ (обычно бывает наоборот, максимум прибыли достигается при меньшем $Q$, чем максимум выручки)
3. $TC(Q_2) < 0$, что также не имеет экономического смысла
P.S. Условие задачи взято из реального учебника экономики
2. Продажа теплиц
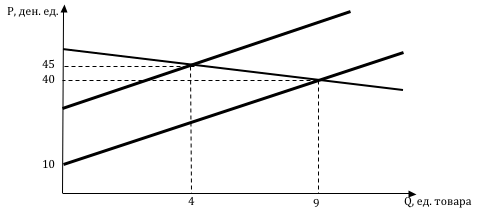
а) Определите, какую максимальную прибыль может получить фирма «Теплон», реализуя теплицы на местном рынке в деревне Огурцово.
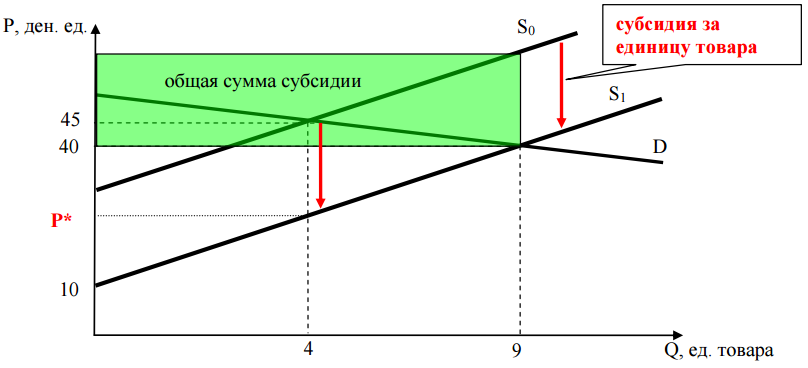
б) У фирмы «Теплон» появилась возможность возить теплицы на продажу в областной центр – город Томатовск, где можно продать любое количество теплиц по цене 60 ден. ед. за штуку. Перевозка теплиц осуществляется грузовыми автомобилями, вместимостью не более 30 теплиц, при этом расходы на перевозку одной машиной составляют 1 ден. ед. на километр пути. Оцените, на каком максимальном расстоянии от деревни Огурцово должен находиться город Томатовск, чтобы фирме «Теплон» было выгодно везти туда теплицы.
б) Заметим, что транспортные затраты являются условно-постоянными, так как будут меняться с увеличением объема перевозок на каждые $30$ единиц продукции. Определим максимально возможный объем продаж фирмы на рынке областного центра, чтобы понять, есть ли риск попасть в зону скачка транспортных затрат, или же мы их можем рассматривать как постоянные. При данных ценах, функциях спроса и затрат объем продаж на рынке областного центра будет максимальным, если транспортные затраты равны нулю. В этом случае фирма выберет такие объемы продаж на местном рынке и рынке областного центра, при которых предельные доходы на этих рынках сравняются. Пусть $MR(Q_1)$ – предельный доход от продажи $Q_1$ единиц продукта $N$ на рынке в Огурцово, $MR(Q_2)$ – предельный доход от продажи $Q_2$ единиц продукта $N$ на рынке Томатовска. Так как рынок Томатовска является для фирмы «Теплон» рынком совершенной конкуренции, то $MR(Q_2) = P$, где $P$ – цена продукта на рынке Томатовска. После того как равенство достигнуто, можно увеличивать объемы продаж только на рынке Томатовска, пока не будет достигнуто равенство предельных доходов и предельных затрат $MC(Q_1 + Q_2) = P = MR(Q_1)$.
Следовательно, нужно решить систему уравнений:
\begin{equation*}
\begin{cases}
MR(Q_1) = P \\
MC(Q_1 + Q_2) = P
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
70 - 10Q_1 = 60 \\
10 + 5(Q_1 + Q_2) = 60
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
Q_1 = 1 \\
Q_2 = 9
\end{cases}
\end{equation*}
Таким образом, максимальный объем, который выгодно поставлять на рынок областного центра в город Томатовск при нулевых транспортных затратах равен $9$ единицам. Так что одной машины вполне достаточно в любом случае, и транспортные затраты можно считать постоянной (не зависящей от объема производства) величиной. А раз так, то их величина не влияет на решение об объемах производства и продаж на рынках. Итак, если фирма принимает решение расширить рынок сбыта и выйти на рынок областного центра, то ей необходимо будет производить $10$ единиц продукции, $9$ из которых следует поставлять на рынок областного центра в город Томатовск, а $1$ продавать на местном рынке в деревне Огурцово. В этом случае прибыль становится равна $9\cdot60 + 1\cdot(70 - 5) - 10\cdot10 - 2,5\cdot100 = 255$ ден. ед., то есть в результате расширения рынка сбыта возрастет на $135$ ден. ед. И следовательно, транспортные затраты не должны превышать этот прирост прибыли. А если транспортные затраты зависят только от расстояния, то $135=1\cdot s$, где $s$ – расстояние.
Следовательно, фирма повезет свою продукцию в Томатовск, если он удален от Огурцово не далее, чем на $135$ км.
3. Выборы и шарики
У каждого гражданина страны есть свое любимое число, и если какой-то из кандидатов предложит именно это число шариков, то избиратель проголосует за него (если любимое число будет предложено обоими кандидатами, гражданин сделает выбор, подбрасывая монетку). Если же любимого избирателем числа не будет среди предложенных вариантов, то он проголосует за того кандидата, который предложит число ближе к его любимому (если разница предложений с любимым числом будет одинаковая, то он тоже подбросит монетку). Самое распространенное любимое число — 50 шариков, его любят 51 человек. 49 и 51 шарик любят по 50 человек, 48 и 52 шарика — по 49 человек, и т. д., 0 и 100 шариков — по 1 человеку. Это распределение любимых чисел известно кандидатам.
Чем закончатся дебаты, если оба кандидата стремятся выиграть выборы?
Дебаты закончатся тем, что оба кандидата назовут число «50».
Если предположить, что это не так, можно показать, что кто-то из кандидатов действует неоптимально для себя. Рассмотрим варианты окончания дебатов, отличные от указанного
выше:
$\bullet$ Если оба кандидата назвали числа, отличные от 50, то
$\circ$ если эти числа находятся на одинаковом расстоянии от 50 (в том числе если они равны), то исход выборов определяется монеткой, но любой кандидат, кто изменит свой выбор на 50, выиграет с определенностью;
$\circ$ если эти числа находятся на разном расстоянии от 50, то победитель выборов определен однозначно, но в этом случае проигравший вел себя неоптимально: назвав число 50, он бы мог выиграть.
$\bullet$ Если один из кандидатов назвал число 50, а другой отличное от 50 число, то второй вел себя неоптимально: так он гарантированно проиграет, а, назвав 50, мог бы выиграть с вероятностью 50%.
Выходит, что в любом исходе, в котором хотя бы кто-то называет число, отличное от 50, кто-то ведет себя неоптимально. С другой стороны, если оба назовут число 50, то судьбу выборов определит монетка, но никто из кандидатов не мог бы повысить свои шансы на победу, назвав что-то другое: если он изменит свой выбор, то гарантированно проиграет.
4. Продажа плантации
Гном Кью хочет купить одну из плантаций, чтобы построить там домик. Эльф Сью в принципе согласен продать, но вопрос только в том, какую плантацию и по какой цене. Приглашенный эксперт оценил альтернативную стоимость каждой унции пыльцы, собираемой с красных цветов, и представил полученную оценку в виде следующих графиков:
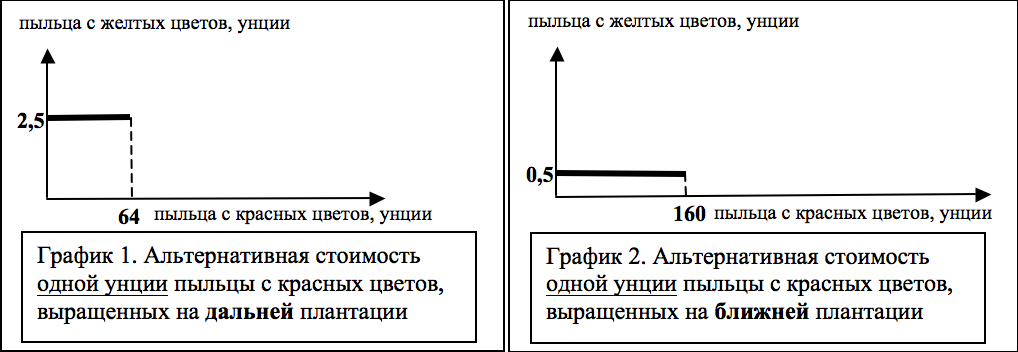
Проанализировав полученные данные, эльф Сью с радостью убедился, что он действительно рационально использует плантации, и сделал интересный вывод: он готов продать любую из плантаций за одну и ту же цену!
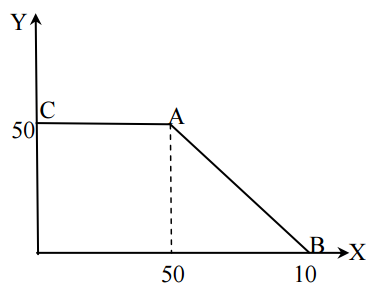
а) Постройте кривую производственных возможностей эльфа Сью до продажи плантации.
б) Найдите, в какой пропорции эльф Сью смешивает цветочную пыльцу, подготавливая ее к продаже.
в) Определите, какую минимальную цену за плантацию должен предложить гном Кью, чтобы эльф Сью согласился на сделку, если известно, что ставка банковского процента стабильна и составляет 5 %.
Для удобства сведем полученные результаты в таблицу:
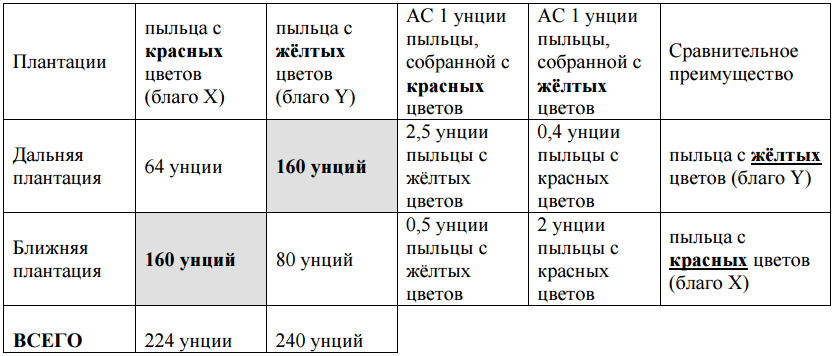
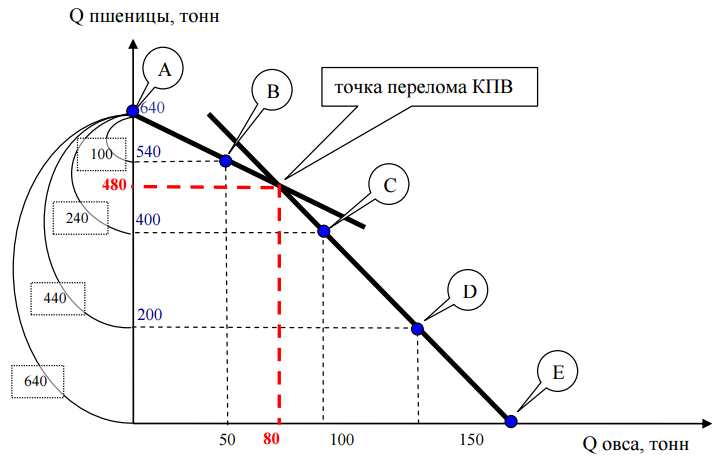
На следующем рисунке представлена КПВ эльфа Сью.
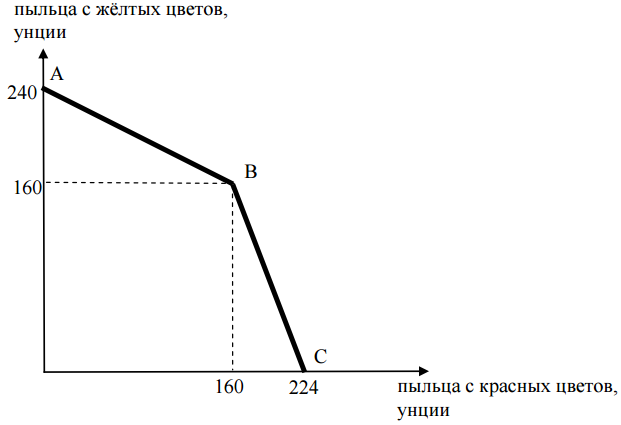
б) Чтобы определить, в какой пропорции рациональный эльф Сью смешивает пыльцу, следует обратить внимание на то, что он готов продать ЛЮБУЮ плантацию за одну и ту же цену, а значит в условиях использования каждой плантации по отдельности он может получить одинаковое количество смеси, годной для продажи. Отсюда можно сделать вывод, что КПВ, построенные для каждой из плантаций в отдельности пересекаются в точке, которая определяет структуру смеси. Аналитически КПВ дальней плантации можно записать так: $Y = 160 - 2,5Х$, а ближней $Y = 80 - 0,5Х$. Точка пересечения имеет координаты $Х = 40$, $Y = 60$, следовательно, эльф Сью смешивает пыльцу в пропорции $2:3$ (две унции пыльцы с красных цветов смешивает с тремя унциями пыльцы с жѐлтых цветов).

в) Зная пропорцию смеси можно записать функцию (назовем ее линией смеси), которая задает все возможные объемы производства смеси $Y = 1,5Х$. А имея сведения о КПВ эльфа Сью, можно рассчитать сколько смеси он ежегодно продает на рынке. Так как точка перелома КПВ имеет координаты $(160,160)$, то это означает, что линия смеси пересечет КПВ на отрезке АВ. (Линия смеси в нашем случае более крутая нежели линия, выходящая из начала координат под углом в 45°.) Нетрудно найти координаты точки пересечения линии смеси и КПВ эльфа Сью. Отрезок АВ лежит на линии, которая описывается функцией $Y = 240 - 0,5Х$ и получается, что эта точка пересечения имеет координаты $(120,180)$, т.е эльф Сью ежегодно готовил и продавал ($120 + 180 = 300$) унций смеси. Когда у него останется одна плантация, то из собранной пыльцы он может приготовить только ($40+60=100$) унций смеси.

Таким образом, лишившись одной плантации, эльф Сью лишается $(300 - 100) \cdot 40 = 8000$ луидоров годового дохода. Он будет готов продать плантацию за сумму $К$, которая компенсирует ему эту потерю дохода, что в условиях стабильности ставки банковского процента может быть определена из соотношения $К \cdot 0,05 = 8000$. Отсюда находим, что $К = \frac{8000}{0,05} = 160 000$ луидоров.