(а) Первый этап. Поиск параметров функции спроса (6 баллов)
Пусть обратная функция спроса задана уравнением $P = a - bQ$ .

Первый способ: Из спроса находим $MR = a - 2bQ$ . Спрос задается линейной функцией (MR убывает), а MC постоянны, значит, условие $MR = MC$ даст максимум. Оптимальный выпуск, равный 18, удовлетворяет этому уравнению, откуда $a - 2b \cdot18 = 10$ .

Второй способ нахождения этого условия в том, чтобы составить функцию прибыли:
$Pr = (a-bQ)Q-10Q$. Это парабола с ветвями вниз, значит, её вершина является максимумом прибыли. Можно приравнять к 0 её производную или найти ответ по формуле вершины параболы, в итоге получим уравнение: $a - 2b \cdot18 = 10$ .
Рассуждения по любому из этих способов оцениваются в 4 балла, из которых 1 балл — обоснование того, что найденная точка является максимумом (убывание MR при постоянстве MC, или рисунок, или вторая производная отрицательна, или ветви параболы вниз). Если допущена арифметическая ошибка, снимается 1 балл, при этом дальнейшее решение оценивается исходя из функции спроса, полученной участником.
При этом цена равна 100, так что $a - b \cdot 18 =100$ (1 балл)
Получаем систему уравнений:
$\begin{cases}
a-36b=10\\
a-18b=100
\end{cases}$
.
Решая её, находим $a = 190 , b = 5$ (1 балл за решение системы)
Значит, спрос описывается уравнением $P = 190 - 5Q$, а $ MR =190- 10Q$

Второй этап. Поиск точки максимума выручки (4 балла)
Первый способ: Поскольку MR — убывающая функция, максимум выручки достигается
там, где $MR = 0$, то есть при $Q = 19$.
Второй способ: Выручка задается функцией:

$TR(Q)=P(Q)\cdot Q=190Q-5Q$² . Это квадратичная парабола с ветвями вниз, значит, ее вершина будет максимумом выручки. Её можно найти по формуле вершины параболы или приравниванием производной к 0, получим $ Q = 19$.

Рассуждения по любому из этих способов оцениваются в 3 балла, из которых 1 балл — обоснование того, что найденная точка является максимумом (убывание MR, или рисунок, или вторая производная отрицательна, или ветви параболы вниз). Политика относительно арифметических ошибок:

• Если на втором этапе решения допущена арифметическая ошибка, в результате которой объем выпуска получился нецелым (что противоречит смыслу задачи) и участник ничего с этим не сделал, то снимается 2 балла из 3.
• Если в результате арифметической ошибки, допущенной на втором этапе решения, получился целочисленный объем выпуска, или же участник, получив нецелый объем, любым способом показал, что он понимает противоречие своего результата условию, то снимается 1 балл из 3.
• Если арифметическая ошибка была допущена на первом этапе решения (и там за нее был снят 1 балл), а второй этап был выполнен (с учетом этой ошибки) правильно, то на втором этапе 1 балл снимается только в том случае, если участник получил нецелый объем выпуска и проигнорировал это несоответствие.

Значит, цена в точке максимума выручки равна $190-5\times19 = 95$ . (1 балл за подсчет ответа)

(б) Уничтожение формы убедило заказчиков в том, что приобретенные ими статуи будут в будущем цениться высоко. Действительно, если бы форма не была уничтожена, то в будущем могли быть отлиты новые экземпляры (это вероятно, учитывая то, что не весь спрос был удовлетворен после того как были отлиты 18 экземпляров). Это сделало бы данную работу скульптора менее редкой и снизило бы ее цену в будущем. Уничтожив форму, скульптор сделал предложение статуй на вторичном рынке заведомо ограниченным, что сделало покупку статуи более выгодным вложением денег в глазах покупателей. Это увеличило их готовность платить, а значит, и прибыль скульптора.

• Каждый экземпляр скульптуры тем более ценен для покупателей, чем меньше всего таких экземпляров — 3 балла
• Повышение ценности и готовности платить за скульптуры (рост спроса) увеличивает прибыль продавца — 2 балла

Рассмотрим сначала ту часть издержек фирмы, которая зависит от t:
$$f(t)=tq+(100-t^2),t∈[0,10]$$
Относительно t это парабола, направленная ветвями вниз, следовательно, минимальное значение на отрезке [0,10] эта функция принимает на одном из краев: либо в точке t=0 (где f(t)=100) либо в точке t=10 (где f(t)=10q). (2 балла)
Видно, что минимум функции на отрезке достигается во второй точке при q<10.
Поэтому если выпуск фирмы меньше 10, то фирма будет располагать свой завод на расстоянии 10 километров от города. И наоборот, если q>10, то фирма будет располагать свой завод непосредственно в городе. При q=10 фирме все равно, в какой из двух точек располагать свой завод: либо в городе, либо максимально далеко от него (в любой из этих точек f(t)=100). (1 балл)
Используя эти соображения, мы теперь можем записать суммарные издержки фирмы как функцию только от ее объема выпуска:
$$TC(q)=\begin{cases}
q^2+10q, & q<10\\
q^2+100, & q\ge10
\end{cases}$$
(1 балл)

Следовательно, функция прибыли фирмы может быть записана следующим образом:
$$Pr(q)=
\begin{cases}
pq-q^2-10q, & q<10\\
pq-q^2-100, & q\ge10
\end{cases}$$
(1 балл)

Каждый из этих участков представляет собой параболу, с ветвями, направленными вниз, что позволяет легко найти максимальное значение прибыли для каждого из участков.
На первом участке максимум прибыли достигается при q=0,5p-5 и составляет
$Pr=(0,5p-5)^2$. (1 балл)
На первом участке максимум прибыли достигается при q=0,5p и составляет
$Pr=0,25p^2-100$. (1 балл)
Первый участок следует выбирать, когда максимальная прибыль на нем больше, чем на втором:
$$(0,5p-5)^2 \ge 0,25p^2-100$$ $$p \le 25 $$

(Идея сравнения двух участков, при условии их корректного выписывания, оценивается в 2 балла, верно найденная граница для цены — еще в 1 балл)
Таким образом, фирме следует выбирать первый участок, когда цена ниже 25 (при этом, если цена падает до 10, то выпуск сокращается до нуля) и выбирать второй участок, когда цена больше 25. Если цена равна 25, то фирме все равно, какой из участков выбирать, так как максимальная прибыль на каждом из них совпадает (в ответе для определенности точка p=25 включена в последний участок):
$$q=
\begin{cases}
0, & p \le 10 \\
0,5p-5, & 10 < p < 25 \\
0,5p, & p \ge 25
\end{cases}$$
(3 балла, если верно указаны все участки. Если забыт нулевой участок, то на один балл меньше. Если в ответе указан только один из участков, то ноль баллов)

(2 балла за рисунок)

Разрыв в функции предложения возникает из-за того, что, когда цена превышает определенный порог, фирме становится выгодно перенести свое производство с периферии непосредственно в город, что обнуляет транспортные расходы и способствует резкому увеличению выпуска.

Комментарий к оцениванию:
Для решения задачи нужно использовать две важные промежуточные идеи:
Завод выгодно располагать либо в самом городе, либо максимально далеко от него. Промежуточные варианты не оптимальны.
Сравнение прибыли, получаемой на двух участках функции прибыли. (Это традиционная олимпиадная идея, которая встречалась, например, и в региональном этапе прошлого года.)
Если ни одна из этих идей не возникла, то задача полностью провалена, и оценить ее можно только нулем баллов.

Ответ
$$q=
\begin{cases}
0, & p \le 10\\
0,5p-5, & 10 < p < 25\\
0,5p, & p \ge 25
\end{cases}$$

а)
1) Найдем численность группы, состоящей из: дети и пенсионеры + выбывшие из состава рабочей силы + безработные = 18+24-8=34 млн. чел. (2 балла)
2) Найдём численность занятых в данной экономике.
Е = население – (дети и пенсионеры + выбывшие из состава рабочей силы + безработные) = 98 – 34 = 64 млн. чел. (2 балла)
3) Найдём число безработных U = часть трудоспособного, которая не работает – выбывших из состава рабочей силы = 24 – 8 = 16 млн. чел. (1 балл)
4) Найдём численность рабочей силы L= E + U = 64 + 16 = 80 млн. чел. (2 балла)
5) Найдём уровень безработицы: $u=\frac{U}{L}*100\%=\frac{16}{80}*100\%=20 \% $ (1 балл)

б)
1) По условию можно определить коэффициент Оукена = $ \beta=\left|\frac{\frac{\Delta Y}{Y^*}*100\%}{\Delta u} \right|=\left| \frac{-2}{1} \right|=2 $
(2 балла)
2) Найдём на сколько процентов вырос ВВП:
Безработица была снижена = 20 – 10 = 10 п.п.(1 балл), следовательно, ВВП вырос на 2х10=20% (2 балла)

3) Тогда, инфляция изменилась на = 20%х1,25 п.п.= + 25 п.п. (2 балла)

Ответ:
А) 20%.
Б) +25 п.п.

Пусть N — количество минут, которые можно использовать телефон Nokia, а S – количество минут, которые можно использовать телефон Samsung. Из условия можно вывести ограничения, которые возможности зарядного устройства и тарифов накладывают на Робинзона: ограничение по зарядке: 2S+N=12, ограничение по тарифам: S+1,5N=12 (2 балла за каждое ограничение — всего 4 балла). Множество доступных распределений — такие точки, которые не выходят за оба ограничения (заштрихованная область) (5 баллов).

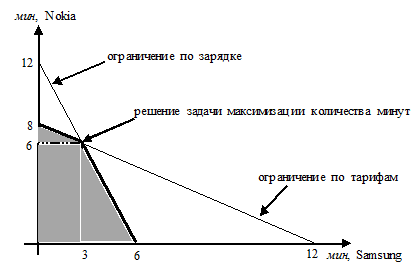
Точка пересечения двух линий — S=3, N=6.

Теперь выберем среди доступных точек такую, где суммарное количество минут максимально (6 баллов за любой из способов).

Первый способ
Можно проверить, что, находясь в точке пересечения ограничений (3;6), Робинзон не может увеличить суммарное количество минут. Действительно, если он захочет увеличить S на X минут, то актуально будет ограничение по зарядке и N уменьшится на 2X минут (то есть S+N уменьшится на X минут). С другой стороны, если он захочет увеличить N на X минут, то актуально будет ограничение по тарифам, и S уменьшится на 1,5X минут (S+N уменьшится на 0,5X минут). Значит, точка (3;6) является оптимальной.

Эти же рассуждения можно провести, начав «двигаться» из одной из угловых точек допустимого множества: (6;0) или (0;8). Сначала движение выгодно (увеличивает S+N), но при достижении точки (3;6) оно перестает быть выгодным, так что (3;6) — оптимальная точка.

Второй способ

Можно графически получить решение задачи максимизации суммарного количества минут. Для этого нарисуем на том же графике несколько линий, N=T-S (линии изображены пунктиром на рисунке). Меняя параметр T, мы изменяем сумму N+S, поскольку N+S=T . Чем дальше лежит пунктирная линия от начала координат, тем больше значение T. Тогда максимально удаленная от начала координат линия, содержащая хотя бы одну точку из допустимых (закрашенная область), лежит в точке пересечений ограничений (3;6). Значит, точка (3;6) является оптимальной.