(а) Если королевство использует только сырье Альфа, то ее кривая производственных возможностей описывается уравнением X+4Y=80. (1 балл)
Если королевство использует только сырье Гамма, то ее кривая производственных возможностей описывается уравнением 2X+Y=80. (1 балл)
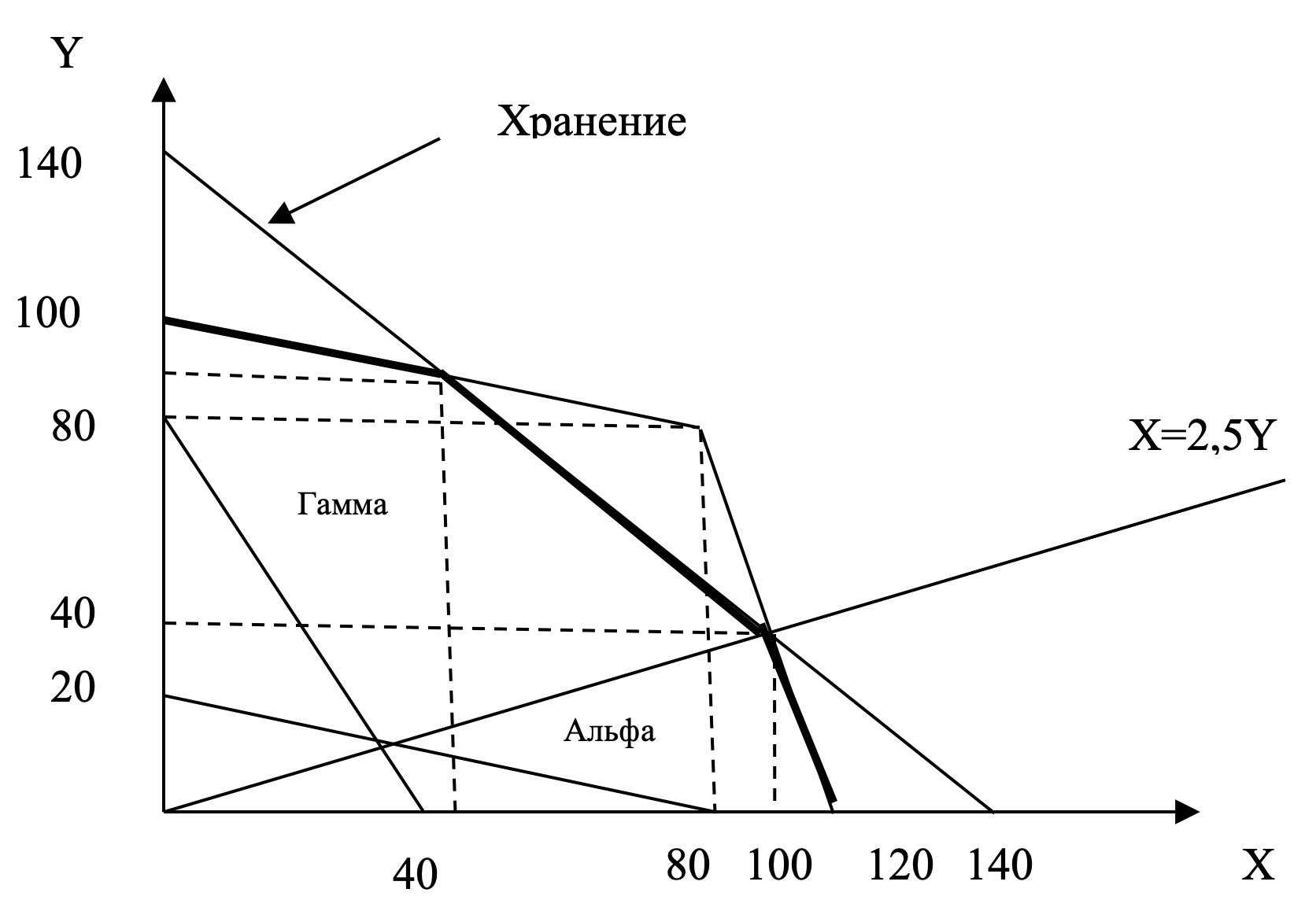
Если бы не было необходимости специального хранения вакцин, то кривая производственных возможностей Панацеи, при условии, что она может пользоваться каждым видом сырья, описывалась бы следующим образом (3 балла):
$\begin{cases} X+4Y=400, \ если \ X≤80\\ 2X+Y=240, \ если \ X>80 \end{cases}$
Поскольку есть необходимость специального хранения вакцин, то имеет место ограничение X+Y≤140. (1 балл) Подобное ограничение приводит к тому, что кривая производственных возможностей Панацеи имеет вид (3 балла):
$ \begin{cases} X+4Y=400,\ если \ X ≤ 160/3 \\ X+Y=140, \ если \ 160/3 < X ≤ 100\\ 2X+Y=240, \ если \ X > 100 \end{cases} $
Построенный верно график оценивается в 2 балла.

(б) Комплект, состоящий из максимального набора вакцин, лежащий на кривой производственных возможностей Панацеи, это комплект, состоящий из 100 об.ед. вакцины Икс и 40 об.ед. вакцины Игрек (1 балл). Следует заметить, что этот комплект лежит на одной из точек излома КПВ.

Если стоимость вакцины Икс будет меньше альтернативных издержек хранения одной единицы вакцины Икс, то Панацее будет выгоднее снижать производство вакцины Икс и увеличивать производство вакцины Игрек. (1 балл)
Таким образом, интервал цен, при котором Панацея будет согласна продавать данный комплект (2 балла):
1≤P≤2, где 1 - альтернативные издержки хранения 1 единицы вакцины Икс, при 160/3<Х<100 и 2 – альтернативные издержки производства 1 единицы вакцины Икс при Х>100.

Так как из того, что $q=\sqrt{L}$ следует, что $L=q^2$ можно записать затраты фирмы на оплату труда как $5*L=5*q^2$. При этом, так как малое предприятие может использовать не больше 4 единиц труда, то его выпуск не превышает двух тонн продукции q≤2. (1 балл)
Рассмотрим сначала ситуацию, когда фирма не сталкивается с налогом. В этом случае прибыль фирмы имеет вид: $pr=pq-5q^2$. Это парабола, с ветвями направленными вниз, и с вершиной в точке q=0,1p. Эта вершина удовлетворяет условию q<2 при p<20. Таким образом, при p<20 оптимально быть малым предприятием, даже если не учитывать налог (а уж с налогом и подавно). (2 балла)
Теперь рассмотрим ситуацию, когда p≥20. В этой ситуации фирме будет выгодно либо производить ровно две тонны продукции (максимальный выпуск, при котором не надо платить налог), либо производить больше двух тонн и платить налог. (2 балла)
Если фирма производит ровно две тонны продукции, то ее прибыль составит
$pr_1=p*2-20=(p-10)*2$. (1 балл)
Если фирма будет производить больше двух тонн, то ее прибыль будет иметь вид
$pr=pq-5q^2-10q$ (относительно q — это парабола с ветвями направленными вниз). (1 балл) Ее максимальное значение будет достигаться в вершине параболы при q=0,1p-1 и составит
$pr_2=p(0,1p-1)-5(0,1p-1)^2-10(0,1p-1)=(p-10)^2*0,05$ (1 балл)
В каком случае фирма решит выбрать первый вариант из двух? В том случае, когда прибыль от него не меньше, чем от второго (3 балла):
$pr_1≥pr_2$
$(p-10)*2≥(p-10)^2*0,05$
С учетом того, что мы рассматриваем ситуацию, когда p≥20, это неравенство легко решить:
2≥(p-10)*0,05
p≤50
Итак, теперь мы знаем, что при цене от 20 до 50 д.е. фирма будет производить ровно две тонны продукции. А при цене больше 50 д.е. ее выпуск составит q=0,1p-1. (2 балла)
Теперь можно записать функцию предложения фирмы:

Ниже представлен требуемый график, на котором жирные линии изображают три участка функции предложения (2 балла):

(а) Пусть бедные получают Х, средний класс – 2Х, а богатые – 4Х. Тогда доход жителей всей страны равен Y=7Х, где Х=1/7 (в долях). Доля каждой группы равна 1/3.(1 балл)
График оценивается в 2 балла.

$$G=\frac{1/2*1*7X-(1/2*1/3*(X+2X+4X)+2*1/3*X+1/3*2X)}{1/2*1*7X}$$ (2 балла)
б) Абсолютное равенство достигается при равенстве доходов после уплаты налогов трех групп населения: $(1-t_{poor}^*)*X=(1-t_{middle}^*)*2X=(1-t_{rich}^*)*4X$ (1 балл)
Определим в общем виде все t* (по 1 баллу).
$(1-t_{poor}^*)*X=(1-t_{middle}^*)*2X$ , получим $t_{middle}^*=1/2(t_{poor}^*+1)$
$(1-t_{poor}^*)*X=(1-t_{rich}^*)*4X$, получим $t_{rich}^*=1/4(t_{poor}^*+3)$

Обозначим $t = t*_{poor}$
$t_{middle}^*=1/2(t+1)$
$t_{rich}^*=1/4(t+3)$
(1 балл) Доходы государства:
Т = t*X+1/2(t+1)*2X+(1/4t+3/4)*4X=3Xt+4X=3/7tY+4/3Y

в) После уплаты налогов все три группы будут получать одинаковый доход. Поэтому коэффициент Джини станет равен нулю. Так как все ценят не только сумму заработанных средств, но и свободное время, то богатые и средний класс могут снижать время работы или вовсе отказываться от дополнительного заработка в пользу свободного времени. В этом случае доходы государства будут сокращаться.(2 балла) В предельном случае, если бы средний класс и богатые отказались вовсе от дополнительного заработка в пользу свободного времени, доходы государства составили бы Т = 3tX, что на 4Х меньше налоговых поступлений в пункте (б).(1 балл)

г) Выразим налоговые поступления (2 балла):
$ 4X*(1/4t+3/4)*(1-2t)+2X*(1/2t+1/2)*(1-2t+2t)+X*t*(1+2t) \rightarrow max$
$7/2-3t \rightarrow max$
t=0

В каждом слагаемом первый множитель – доход (4Х, 2Х, Х); второй множитель – ставка налога, посчитанная в предыдущем пункте; третий множитель – доля людей, перешедшая в более бедную группу и пришедшая из более богатой группы.
Значит, оптимальные налоги на богатых – 75%, на средний класс – 50%, на бедных – 0%, ни один из индивидов не перейдет в другую социальную группу (1 балл).

(а) Условия максимизации прибыли в условиях совершенной конкуренции: $р=МС$. $МС=2$ д.е. за тыс. км. Следовательно, $Р=2$ (1 балл). При данной функции спроса:
$2=21-0,001Q$, $Q=19000$. (1 балл) Так как производственные мощности фирм равны 1000 тыс. км в год, то на рынке будет действовать не менее $N=19$ фирм. (1 балл)

(б) Так как количество фирм ограничено 15, то это значит, что введено ограничение на объем перевозок $Q=15000$ км в год (1 балл) (так как сохраняется ограничение на производственные мощности фирм). При введении квоты на рынке возникает дефицит, который приводит к росту цен. Для данного объема перевозок из функции спроса определяется тариф $Р=21-0,001\cdot15000 Р=6$ (1 балл). Прибыль каждой фирмы будет: $П=6\cdot1000-2\cdot1000=4000$. Прибыль всех фирм – 60000 тыс. д.е. (1 балл)

(в) Лицензию имеет смысл перепродать по цене, не меньшей ее текущей ценности $4000/0{,}1=40000$ д.е. (2 балла)
Также верной является следующая запись:
$\frac{4000}{1+0,1}+\frac{4000}{(1+0,1)^2}+ \dots + \frac{4000}{(1+0,1)^n}=40000$, где n стремится к бесконечности.

Фирма, купившая лицензию на вторичном рынке не получит положительной экономической прибыли, так как заплатит ее за лицензию. (1 балл)

(г) Если производственные мощности фирмы 2000 тыс. км в год, то можно ожидать, что фирма будет участвовать в аукционе, так как данная фирма поучит большую отдачу от лицензии, чем другие фирмы. (1 балл),
На рынке остается 15 фирм. Если новая фирма будет функционировать на рынке, то новое равновесие будет при цене $Р=21-0,001\cdot (14\cdot 1000+2000)=5$. (1 балл) Прибыль новой фирмы будет: $П=5\cdot2000-2\cdot2000=6000$, а прибыль каждой из остальных фирм будет равна 3000. Если предположить, что государству неизвестны особенности технологий, а на аукционе выигрывает участник, предложивший большую цену, то низкопроизводительные фирмы смогут предложить 30000 д.е. за лицензию, а высокопроизводительная фирма немного больше, при этом точно выиграв аукцион. При этом она получит положительную экономическую прибыль не более 30000 д.е. (1 балл)

(д) Если фирмы решили совместно определять свой объем перевозок, то они стали монополией (организовали картель). (1 балл) Условие максимизации прибыли: $MR=MC$. $MR=21-0,002Q$. Так как $МС=2$, то условие максимизации прибыли $2=21-0,002Q$. Так как предельные издержки постоянны, а предельная выручка является убывающей функцией, то найденные параметры равновесия максимизируют прибыль. $Q^*=9500$, $Р^*=11{,}5$ (1 балл) $П=11,5\cdot9500-2\cdot9500=90250$. В среднем на каждую фирму приходится $90250/15=6017$ д.е. (1 балл)
Верным также является запись функции прибыли.