1. Задача про кломпы
Спрос и предложение рынка заданы функциями QD=120-3P, QS=20+P
1. При какой цене и объеме продаж кломпов рынок находится в равновесии?
2. Ожидается, что в ближайшее время предложение снизится на 20%, а спрос увеличится на 50%. Какими станут цена и объем продаж?
Одна из фирм, которая производит кломпы, в настоящее время хочет увеличить выручку от продажи на 5%. Известно, что эластичность спроса по цене такова, что увеличение цены на 1% приводит к уменьшению спроса на 2%.
3. На сколько процентов нужно поднять или опустить цену, чтобы добиться требуемого увеличения выручки?
Одним из показателей концентрации рынка является индекс Херфиндаля-Хиршмана. Он представляет собой сумму квадратов долей продаж (в процентах) всех присутствующих на рынке фирм. Антимонопольная служба разрешает бесконтрольные слияния и поглощения на рынке до достижения индексом значения 1800.
На рынке кломпов Голландии присутствует 20 практически одинаковых фирм, имеющих одинаковые доли продаж. Одна из фирм стремится к расширению за счет присоединения к себе других.
4. Какое количество других фирм она может присоединить к себе так, чтобы индекс не превысил допустимого значения?
Увеличение спроса и снижение предложения отразится на функциях следующим образом QD=1,5(120-3P)=180-4,5Р, QS=0,8(20+P)=16+0,8Р
2. Пересечение новых функций дает новые параметры равновесия 180-4,5Р=16+0,8Р,
P=30,9 Q=40,7
3. Коэффициент эластичности -2=ΔQ/ΔP
Связь между изменениями цены и объема ΔQ =-2ΔP
Увеличение выручки на 5% означает, что TR2=1,05TR1
TR2=1,05P1Q1=P2Q2
P2=(1-ΔP)P1
Q2=(1+ΔQ)Q1=(1+2ΔP)Q1
TR2=(1-ΔP)P1(1+2ΔP)Q1=1,05P1Q1
(1-ΔP)(1+2ΔP)=1,05
Решение квадратного уравнения дает ΔP=0,055 снижение цены на 5,5%
4. 20 фирм имеют по 5 % доли рынка
Х – количество объединившихся фирм,
тогда индекс = (5х)2+(20-х)52=1800
х=7 одна фирма может присоединить еще 6
2. Фирма «Велла»
службы 5 лет. (Амортизация оборудования рассчитывается по линейной схеме.) В течение года фирма производит 400 тыс. штук модульных упаковок данного размера.
1. Какой должна быть рыночная цена этой продукции, чтобы фирма достигла уровня безубыточности?
2. Если цена на картонную модульную коробку данного размера установилась на уровне 4 руб., то каковы финансовые результаты фирмы (прибыль или убытки и в каком размере)
ATC=TC/Q
При линейной схеме амортизации выплаты ежегодные составят 106/5=200000
Общие затраты= 200000+100000+350000+50000+200000=900000
При Q=400000 ATC=P=2,25
Если P=4, то прибыль на единицу продукции составит 1,75 рубля, а на всю партию из 400000 штук 700 тыс. руб.
3. Сено для царя Тридевятого Царства (2)
Известно, что спрос на сено в этом сезоне составляет 25 пудов. Прибыль от выпаса коров составляет 2 рубль с десятины, при этом каждый боярин при равенстве выгоды предпочтёт поставлять сено ко двору, а не заниматься коровами. Необходимо определить, заполнив пустые столбцы в таблице:
- Какие луга будут использоваться в этом сезоне;
- Какие из лугов будут использоваться полностью, а какие – частично (в этом случае необходимо указать долю, учитывая, что при частичном использовании луга его остаток будет использован для выпаса коров);
- Прибыли каждого из бояр-владельцев от продажи сена.
| № луга | Урожай с десятины | Затраты на обработку десятины | Используется (да/нет/размер доли) | Прибыль |
|---|---|---|---|---|
| 1 | 1 | 2 | ||
| 2 | 3 | 2 | ||
| 3 | 5 | 2 | ||
| 4 | 2 | 2 | ||
| 5 | 4 | 2 | ||
| 6 | 5 | 3 | ||
| 7 | 3 | 3 | ||
| 8 | 1 | 3 | ||
| 9 | 4 | 3 | ||
| 10 | 2 | 3 |
| № луга | Урожай с десятины | Затраты на обработку десятины | Минимальная необходимая выручка | Минимальная возможная цена | Объём предложения |
|---|---|---|---|---|---|
| 3 | 5 | 2 | 4 | 0,8 | 5 |
| 5 | 4 | 2 | 4 | 1 | 9 |
| 6 | 5 | 3 | 5 | 1 | 14 |
| 9 | 4 | 3 | 5 | 1,25 | 18 |
| 2 | 3 | 2 | 4 | 1,(3) | 21 |
| 7 | 3 | 3 | 5 | 1,(6) | 24 |
| 4 | 2 | 2 | 4 | 2 | 26 |
| 10 | 2 | 3 | 5 | 2,5 | 28 |
| 1 | 1 | 2 | 4 | 4 | 29 |
| 8 | 1 | 3 | 5 | 5 | 30 |
Поскольку спрос на сено составляет 25 пудов, последним из вовлечённых в торговлю сеном бояр окажется владелец участка № 4, а цена установится на уровне 2 рублей за пуд. Участки № 1, № 8 и № 10 не будут использоваться для поставок сена, поскольку минимально возможные для их хозяев цены сена превышает 2 рубля. Участок № 4 будет использоваться частично, поскольку от него будет требоваться только 1 дополнительный пуд, а при обработке всего участка будет выращено 2 пуда. Все остальные участки будут использоваться полностью.
Прибыль от продажи сена рассчитывается как урожай, умноженный на цену сена, за вычетом расходов на обработку. Для участка № 4 эту величину необходимо уменьшить вдвое вследствие того, что будет обрабатываться только половина участка.
| № луга | Урожай с десятины | Затраты на обработку десятины | Используется (да/нет/размер доли) | Прибыль |
|---|---|---|---|---|
| 1 | 1 | 2 | нет | 0 |
| 2 | 3 | 2 | да, полностью | 4 |
| 3 | 5 | 2 | да, полностью | 8 |
| 4 | 2 | 2 | да, 50% | 1 |
| 5 | 4 | 2 | да, полностью | 6 |
| 6 | 5 | 3 | да, полностью | 7 |
| 7 | 3 | 3 | да, полностью | 3 |
| 8 | 1 | 3 | нет | 0 |
| 9 | 4 | 3 | да, полностью | 5 |
| 10 | 2 | 3 | нет | 0 |
4. Инфляция 1996 года
На графике приведены значения инфляции в процентах за каждый месяц в течение всего этого года. (По оси Y отложены значения уровня инфляции в процентах).
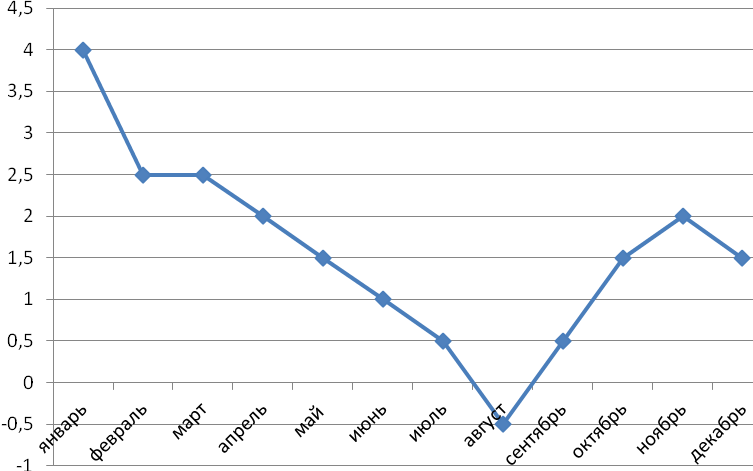
1. Вычислите значение уровня инфляции за год в процентах.
2. Определите, удалось ли государству выполнить поставленную задачу и снизить инфляцию до желаемого уровня, если было расхождение, то, сколько процентов оно составило.
3. Вычислите темп инфляции, если известно, что в 1995 г. ее уровень составил 131,5%, приняв его за базовый.
(Ответ округлите до сотых).
Да, государство справилось с инфляцией: реальная инфляция оказалась на (14%-10,97%)=3,03% ниже, чем заявленная.
(10,97-131,5)/131,5×100%≈-91,66%
5. Фирма "Тедди"
Какую прибыль получит фирма, если рассчитывает выпускать в месяц 1000 игрушек, а рыночная цена 400 рублей за одну игрушку?
прибыль=1000×400-(200000+1000×100)=100000