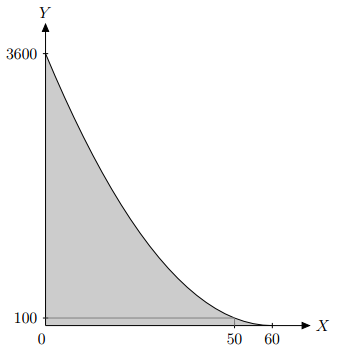
1. Тройные бутерброды
а) Запишите уравнение кривой производственных возможностей страны Гамма и изобразите КПВ на графике.
б) Предположим, распределение ресурса между производством товаров осуществляется мудрым правителем, который заботится только о благосостоянии граждан. Сколько бутербродов съедят жители страны Гамма? Отметьте соответствующую точку на КПВ.
в) Жители страны Гамма узнали, что бутерброд станет вдвойне вкусней, если намазать на него еще единицу товара $Z$. Технология производства товара $Z$ неизвестна, но производители страны Дельта готовы продать товар $Z$ по цене 2 единицы товара $X$ за штуку. Мудрый правитель решил, что теперь жители страны Гамма будут есть только бутерброды «$X+2Y+Z$». Сколько бутербродов они съедят?
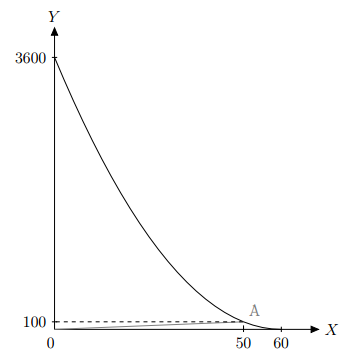
б) Находим на этой кривой точку $2X=Y$, получаем $X=50$, $Y=100$. Это соответствует 50 бутербродам.
в) Пусть $x$ — экспорт товара $X$. Тогда $Z=x/2$. Кроме того, в соответствии с пропорциями бутерброда, $2X=Y=2Z$, а также из КПВ $(X+x)+\sqrt{Y}=60$. Получаем систему из 4 уравнений с 4 неизвестными, она решается:
\begin{align*}
X=Z=18, && Y=36, && x=36.
\end{align*}
Получается, что жители съедят 18 бутербробов.
Критерии
а) (5 баллов)
3 балла за уравнение КПВ и 2 балла за график
б) (7 баллов)
4 балла за верную пропорцию, 3 балла за решение с этой пропорцией.
Снимается 1 балл за арифметическую ошибку.
Снимается 4 балла, если пропорция рассчитана наоборот ($X=2Y$).
Снимается 2 балла, если точка найдена, но не отмечена на графике.
в) (8 баллов)
4 балла за систему уравнений (возможно, с другими обозначениями) и 4 балла за ее решение.
Снимается 1 балл за арифметическую ошибку.
2. Три страны
| Страна | Спрос | Предложение |
|---|---|---|
| 1 | $Q_1=100-p$ | $Q_1=p$ |
| 2 | $Q_2=200-p$ | $Q_2=p$ |
| 3 | $Q_3=400-p$ | $Q_3=p$ |
а) Предположим, что страны образовали Таможенный союз, и появился общий совершенно конкурентный рынок\\ пшеницы. Найдите равновесие на этом рынке, указав равновесную цену, объемы потребления, производства и импорта (экспорта) в каждой из стран.
б) Укажите страны, потребители внутри которых выиграли от начала международной торговли. В каких странах от начала международной торговли выиграли производители? Объясните свои ответы.
в) Предположим, что страна 3 ввела импортную пошлину в размере 50. Найдите новое равновесие и укажите, как эта мера сказалась на потребителях и производителях в каждой стране по сравнению с пунктом б).
| Страна | Спрос | Предложение | Импорт/экспорт |
| 1 | $ Q_1=0$ | $Q_1=120$ | $Ex=120$ |
| 2 | $ Q_2=80$ | $Q_2=120$ | $Ex=40$ |
| 3 | $ Q_3=280$ | $Q_3=120$ | $Im=160$ |
б) Потребители выигрывают, если покупают товар дешевле, чем раньше, и проигрывают, если покупают его дороже. Производители выигрывают, если продают товар дороже, чем раньше, и проигрывают, если продают его дешевле.
Найдем внутреннее равновесие (до торговли) в каждой стране, приравняв спрос и предложение:
| Страна | $p$ | $Q$ |
| 1 | 50 | 50 |
| 2 | 100 | 100 |
| 3 | 200 | 200 |
Составим таблицу:
| Страна | Потребители | Производители |
| 1 | Проиграли | Выиграли |
| 2 | Проиграли | Выиграли |
| 3 | Выиграли | Проиграли |
в) После введения импортной пошлины цена в стране 3 должна быть на 50 выше, чем в других странах: $p_3=p_1+50=p_2+50$. Тогда новые функции спроса и предложения ($p=p_1=p_2$):
| Страна | Спрос | Предложение |
| 1 | $ Q_1=100-p$ | $Q_1=p$ |
| 2 | $ Q_2=200-p$ | $Q_2=p$ |
| 3 | $ Q_3=400-(p+50)$ | $Q_3=p+50$ |
Повторяя решение пункта а), находим равновесную цену $p=100$ (это цена в странах 1 и 2, в стране 3 цена 150). Тогда, подставляя в спрос и предложение, получаем:
| Страна | Спрос | Предложение | Импорт/экспорт |
| 1 | $ Q_1=0$ | $Q_1=100$ | $Ex=100$ |
| 2 | $ Q_2=100$ | $Q_2=100$ | $Ex=Im=0$ |
| 3 | $ Q_3=250$ | $Q_3=150$ | $Im=100$ |
Рассуждая аналогично пункту в), получаем:
| Страна | Потребители | Производители |
| 1 | Без изменения | Проиграли |
| 2 | Выиграли | Проиграли |
| 3 | Проиграли | Выиграли |
Критерии
а)(7 баллов)
4 балла за правильное нахождение равновесия (решение уравнения), по 1 баллу за ответы для каждой страны.
Если выписан только ответ, то ставится 1 балл за весь пункт.
б)(3 балла)
По 1 баллу за обоснованный ответ для каждой страны. За ответы без обоснования ставится 0 баллов.
Если результаты были основаны на неверных расчетах в пункте а), то за пункт б) ставится 0.
в) (10 баллов)
4 балла за нахождение равновесия (решение уравнения), по 1 баллу за ответы для каждой страны, по 1 баллу для каждой страны за рассуждения о благосостоянии (если обоснование было дано в б), то здесь его можно не повторять).
3. Электроники-11
Администрация города N согласна купить у фирмы «Электроник-N» не более 800 тыс. $кВт\cdotч$ в месяц по цене не более 12 руб. Частная производственная фирма может купить у фирмы не более 500 тыс. $кВт\cdotч$ в месяц по цене не более 16 руб. Других клиентов у фирмы нет.
а) Если «Электроник-N» может назначить разные цены для разных потребителей, то сколько электроэнергии он будет производить и продавать? Какую прибыль он получит?
б) Рассмотрим фирму «Электроник-А». Производство обходится ей в 7 руб. за $кВт\cdot ч$ (производственные мощности не ограничены, других издержек нет). Раньше она могла продавать электроэнергию только по единой фиксированной цене 15 руб. за $кВт\cdot ч$, но недавно администрация сняла это ограничение, и теперь «Электроник-А» может назначить любую (единую) цену для всех своих покупателей. Сама администрация города А готова купить у фирмы не более 1 000 тыс. $кВт\cdot ч$ по цене не более 15 руб. за $кВт\cdot ч$. Также спрос предъявляет фирма «Электроник-N», а других покупателей нет. Какую цену назначит фирма «Электроник-А» и какую максимальную прибыль получит?
в) Мэр города N может лишить лицензии фирму «Электорник-N», начиная со следующего месяца, если фирма «Электорник-А» даст ему взятку. В этом случае фирма «Электорник-А» получит прямой доступ к конечным потребителям в городе N, но по-прежнему должна будет назначать единую цену для всех своих потребителей. Какую максимальную взятку согласится дать фирма «Электорник-А»?
Утверждение 1. Нет смысла продавать энергию по ценам, отличным от 16 и 12. Действительно, если поставить цену из множества $P\in [0;12)\cap (12;16)$, то повышение цены не уменьшит спрос, то есть выручка увеличится без изменения издержек, а значит, увеличится прибыль.
Утверждение 2. Нет смысла продавать более 1000 тыс. единиц продукции. Допустим, мы продали больше 1000 тыс. единиц продукции. Это значит, что мы продаем товар обоим покупателям и используем оба источника при производстве (собственное производство и закупки). Тогда, если мы продадим администрации на одну тыс. единиц меньше, отказавшись от закупки этой тысячи у фирмы «Элекироник-А», то наша прибыль увеличится на 3.
Утверждение 3. Нет смысла закупать электроэнергию у фирмы «Электроник-А». Поскольку мы продаем не более 1000 тыс. единиц продукции, мы можем произвести их все самостоятельно, понеся издержки $TC(q)=2000+10q$ тыс. руб. Если же мы будем закупать энергию в другом городе (сэкономив 2000 тыс. рублей, но заплатив больше за каждую единицу), то издержки составят $15q$ тыс. Нетрудно убедиться, что закупки извне оправданы только при $q\le 400$, но это не может быть оптимальным объемом продаж, так как производственная фирма готова купить 500 единиц по цене 16, что превышает издержки в любом случае.
Поскольку готовность платить каждого покупателя не убывает по цене, нужно назначить каждому из них ту максимальную цену, которую он готов платить: производственной фирме $P_1=16$, а администрации $P_2=12$. При этом из доказанного выше следует, что мы должны произвести всю энергию сами и продать ее производственной фирме и администрации. Поскольку обе цены превышают предельные издержки, ясно, что нужно произвести так много энергии, как это возможно — 1000 тыс. единиц, и продать 500 из них по максимальной цене $P_1$, а остальные — по цене $P_2$. Прибыль, которую можно получить таким образом, равна 2000 тыс руб.
б) Рассмотрим оптимальное поведение фирмы «Электроник-N» в зависимости от цены $P_A$, по которой фирма «Электроник-A» будет продавать ей энергию.
Если $P_A<12$, то фирма «Электроник-N» захочет купить «Электроник-A» все 1300 тыс. единиц, которые она может продать. Это следует, во-первых, из того, что 1300 тыс. единиц можно продать по цене не меньше 12 (значит, она захочет продать все), а кроме того, даже производство всех возможых 1000 тыс. единиц на своих мощностях не окупит связанных с этим квазипостоянных издержек: $2000+10\times 1000>P_A\times 1000$.
Если $P_A=12$, то фирме «Электроник-N» без разницы, закупать 1000 тыс. единиц или производить самостоятельно. При этом она может продать 500 тыс. единиц по цене 16 производственной фирме, а также любое количество энергии администрации города N. Таким образом, спрос фирмы «Электроник-N» на продукцию фирмы «Электроник-A» будет иметь следующий вид (в тысячах единиц):
$$Q= \begin{cases}
0, & \text{если } P_A>12; \\
1300, & \text{если } 0 \le P_A \le 12.
\end{cases}$$
Прибавив к этому спрос, предъявляемый администрацией города A, получим
$$ Q= \begin{cases}
0, & \text{если } P_A>15; \\
1000, & \text{если } 12 < P_A \le 15; \\
2300, & \text{если } 0 \le P_A \le 12.
\end{cases}$$
Фирма A может либо назначить цену 15 и получить прибыль $(15 -7)\times 1000 = 8000$ тыс. руб., либо назначить цену 12 и получить прибыль $(12-7)\times 2300 = 11500$ тыс. руб. Предпочтительнее второй вариант.
в) Функция спроса, с которой столкнется фирма «Электроник-A» при таком развитии событий, имеет вид:
$$ \begin{cases}
0, & \text{если } P>16; \\
500, & \text{если } 15 < P \le 16;\\
1500, & \text{если } 12 < P \le 15; \\
2300, & \text{если } 0 \le P \le 12.
\end{cases}$$
Сравним прибыли при различных ценах:
| $P$ | $\pi$ |
| 16 | $(16-7)\times 500 = 4500$ |
| 15 | $(15-7)\times 1500 = 12000$ |
| 12 | $(12-7)\times 2300 = 11500$ |
Цена 15 приносит наибольшую прибыль, которая на 500 больше, чем в случае без взятки. Значит, максимальная взятка равна 500.
Критерии
Решения, приводимые участниками, могут отличаться от приведенного выше (например, вряд ли стоит ждать от них предварительного доказательства приведенных утверждений), но проверяющий должен определить, какие необходимые шаги выполнены в решении, а какие нет
а) (10 баллов)
Если в ходе решения участника приведено и доказано то, что выше называется Утверждение 1, он получает 2 балла.
Если в ходе решения участника приведено и доказано то, что выше называется Утверждение 2, он получает 3 балла.
Если в ходе решения участника приведено и доказано то, что выше называется Утверждение 3, он получает 3 балла.
Верный ответ оценивается в 2 балла
б) (10 баллов)
Если правильно найдена пограничная точка спроса фирмы «Электроник-N» ($P_A=12$), то ставится 4 балла.
Еще 6 баллов ставится за корректную функцию спроса на продукцию фирмы «Электроник-A» и выбор оптимальной цены. Из них:
-
\item 4 балла, если построен корректный спрос, включая точку $P_A=15$.
\item 2 балла за сравнение вариантов цен, которые участник не получит, если допустил арифметическую ошибку, повлиявшую на результат сравнения.
За каждую арифметическую ошибку снимается 1 балл.
в) (5 баллов)
Правильная функция спроса оценивается в 2 балла.
Правильный расчет прибылей оценивается в 1 балл.
Сравнение прибылей и верный ответ про взятку оценивается в 2 балла.
Политика относительно арифметических ошибок аналогична пункту б).
4. Сговор и потолок
Приглашенный консультант (которому известно не больше) посоветовал службе хитрый ход — ввести потолок цены и посмотреть, как отреагирует рынок. «В ряде случаев, — заявил консультант, — по изменению рыночной цены и объема продаж я смогу точно определить, есть ли на рынке сговор».
Когда полоток цены был введен, консультант смог точно определить, есть ли на рынке сговор. Есть ли на рынке сговор?
Примечание: для простоты будем считать, что при сговоре картель фирм ведет себя как монополист, а в отсутствие сговора поведение фирм совершенно-конкурентное.
Если потолок цены вводится на конкурентном рынке, то он обязательно уменьшит объем продаж, который теперь будет определяться величиной предложения. Для монополии это неверно: если потолок цены вводится на уровне выше точки $MR=MC$, то объем выпуска растет. Это видно из следующего графика:
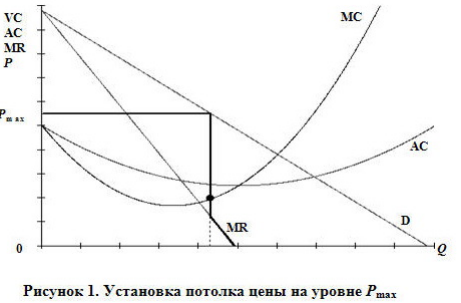
Если потолок опустится ниже уровня точки $MR=MC$, то выпуск будет ниже первоначального равновесия.
Таким образом, если при вводе потолка цены объем продаж на рынке снизился, то сделать вывод о рыночной структуре невозможно, а если вырос, то можно говорить о монополии. Если эксперту удалось сделать такой вывод, то на рынке был сговор.
Критерии
Только правильный ответ оценивается в 1 балл.
Ответ на вопрос о том, как объем выпуска монополии зависит от потолка цены (например, с помощью график оценивается в 10 баллов.
Если доказано только достаточное условие выявления сговора, но не критерий (то есть показано, что при монополии выпуск может вырасти, но не показано, что он может снизиться в обоих случаях), снимается 5 баллов.
5. Корреляция без причины — признак дурачины
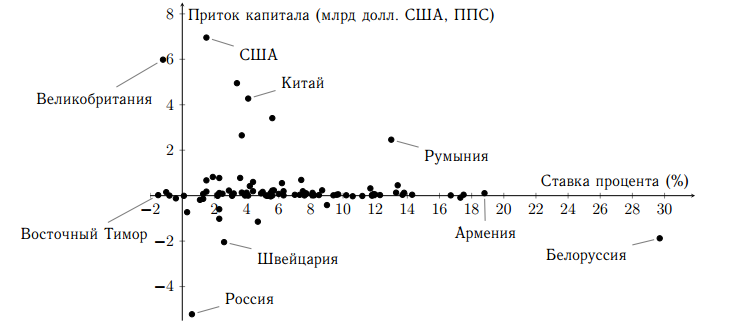
Можно видеть, что множество стран с совершенно разными реальными процентными ставками имеют примерно одинаковое сальдо счета движения капитала. С другой стороны, почти все страны с большим притоком капитала имеют невысокие процентные ставки, а из страны с самой высокой процентной ставкой наблюдается отток капитала.
Более того, между ставкой процента и сальдо счета движения капитала существует небольшая отрицательная корреляция, то есть в среднем чем больше ставка, тем меньше чистый приток капитала. Эти наблюдения противоречат изначальной интуиции. Как можно объяснить это противоречие?
Критерии
За идею нарушения «при прочих равных» — 10 баллов, за объяснение отрицательной корреляции через риски — 10 баллов.
Если участник не набрал 20 баллов по предыдущему критерию, но привел какие-то другие аргументы, имеющие право на существование (например, смещенная выборка 95 стран), то он получает по 4 балла за каждый такой аргумент.