1. Капрезе
На рисунке представлены бюджетные ограничения до, между и после этих событий. Точки A, B и C на рисунке — точки выбора бабы Вали при разных ситуациях.
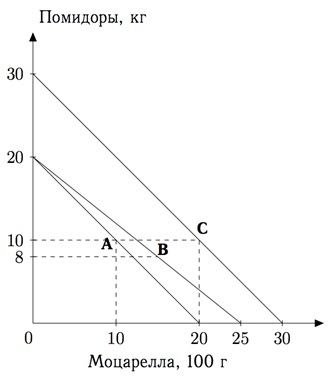
а) Укажите ситуации, которым соответствует каждая из этих трех точек. Объясните ваши ответы.
б) Посчитайте расходы бабы Вали на моцареллу в каждом случае.
в) Внучка подарила бабе Вале бутылку оливкого масла и посоветовала есть помидоры и моцареллу только в составе салата капрезе (нужно взять одинаковые по весу количества помидор и моцареллы и добавить немного масла). Бабе Вале так понравился салат, что она решила есть только его, причем как можно больше. Отметьте на графике выбор бабы Вали после повышения пенсии и укажите координаты отмеченной точки.
2. Жульен из мухоморов
Король гномов Урфин IV, фанатичный сторонник здорового образа жизни, решил ограничить потребление населением этих грибов, полагая, что такая традиция уже не первое столетие не лучшим образом сказывается на здоровье гномов. Не долго думая, он объявил, что, начиная с будущего понедельника, все продавцы мухоморового жульена должны будут платить налог по 3 ден. ед. за каждую проданную порцию.
На следующий день к Урфину пришел его министр финансов, фанатичный противник госдолга, и сказал:
Ваше Величество! Ваше решение, как всегда, гениально, однако в результате введения такого налога потребление сократится только лишь на 8 тыс. порций в месяц. Сейчас каждый месяц продается 28 тыс. порций по 5 ден. ед., а эластичность предложения в точке равновесия в 2 раза превышает эластичность спроса (по модулю). Я знаю, какой должна быть величина налога, чтобы еще больше сократить потребление и максимально увеличить доходы казны. И тогда мы, наконец, сможем вернуть весь наш долг эльфийскому королю!
Какую величину фиксированного потоварного налога рекомендовал ввести министр финансов?
Доказательство:
Если $|E_S|=2|E_D|$, то есть $|(∂Q_S)/∂P \cdot P^e/Q^e |=2 \cdot |(∂Q_D)/∂P \cdot P^e/Q^e |$, то угловой коэффициент функции предложения в 2 раза превышает угловой коэффициент функции спроса:$ Q_D=a-bP, Q_S=c+2bP.$ Тогда равновесная цена определяется как $P_0^e=(a-c)/3b.$
Если вводится налог в размере Т ден. ед., уплачиваемый производителями, то $Q_D=a-bP, Q_S=c+2b(P-T) \ и \ P_1^e=(a-c)/3b+2/3 T=P_0^e+2/3 T.$
Следовательно, при Т=3 новая цена равна 7 ден. ед., а новое равновесное количество 20 тыс. порций (см. рис.)
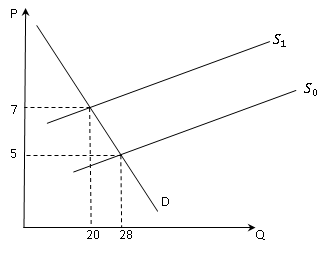
Теперь, зная координаты двух точек на линейной функции спроса, можем определить ее вид: $Q_D=48-4P.$ Угловой коэффициент функции предложения равен 8, и координат исходной точки равновесия достаточно, чтобы определить вид функции $S_0: Q_S=-12+8P.$
Теперь не трудно определить величину налога, максимизирующего налоговые сборы.
Пусть величина потоварного налога равна Т ден. ед. Тогда $Q_S=-12+8(P-T)$, функция спроса не меняется, а равновесное количество определяется Q^e=28-8/3 T. Максимизируем функцию налоговых поступлений: $TQ^e=28T-8/3 T^2→max!$
$28-16/3 T=0 →T=5,25$
3. Заемные средства и оптимум фирмы
а) Допустим, $r_c=r_d=10\%$. Найдите оптимальный выпуск фирмы как функцию от L. Постройте график этой функции.
б) Допустим, $r_c=20\%, r_d=10$. Найдите оптимальный выпуск фирмы как функцию от L. Постройте график этой функции.
Если для выпуска данной единицы нужно привлекать заемные средства, то кроме этих 20 д.е. фирме придется заплатить и процент: $r_c \cdot 20=0,1 \cdot 20=2$д.е. Итого предельные издержки составят 22 д.е.
Если для выпуска данной единицы не нужно привлекать заемные средства, то производя эту единицу, фирма потеряет процент, который она могла бы получить, держа средства на депозите: $r_d \cdot 20=0,1 \cdot 20=2$д.е. Итого предельные издержки составят 22 д.е.
Таким образом, независимо от L, предельные издержки фирмы постоянны и равны 22 д.е.
Функция предельного дохода также не зависит от L: $MR=52-2Q$.
Пересекая предельный доход и предельные издержки, получаем, что, независимо от L, оптимальный выпуск равен 15. Итак, $Q^*(L)=const=15$
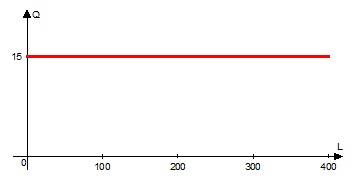
(б). Вновь найдем (при данном L), функцию предельных издержек фирмы. Производственные издержки равны 20. Допустим, фирма решает произвести Q единиц продукции. Если денег хватает (при $20Q\le L$), то фирма при производстве дополнительной единицы продукции теряет процент по депозитам. Предельные издержки равны $(1+r_c) \cdot 20=24$д.е. Если приходится привлекать заемные средства (при $20Q\ge L$), то фирма при производстве дополнительной единицы продукции платит процент по кредиту, и предельные издержки равны д.е.
Таким образом, функция предельных издержек имеет вид
$$MC(Q)=\begin{cases}
22, & Q<\frac{L}{20}\\
24 & Q>\frac{L}{20}
\end{cases}$$
График этой функции представляет собой «лесенку» из двух ступенек, причем точка перехода с нижней ступеньки на верхнюю зависит от L. Нарисуем пунктиром также вертикальную линию, соединяющую две ступеньки в точке $Q=\frac{L}{20}$.
При больших L (насколько больших, скажем ниже) точка пересечения графиков и будет находиться на нижней ступеньке:
$MR=52-2Q=22$, откуда $Q=15$. Это возможно, пока $15\le \frac{L}{20}$, то есть $L \ge 300$.
При маленьких L(насколько маленьких, скажем ниже) точка пересечения графиков и будет находиться на верхней ступеньке:
$MR=52-2Q=24$, откуда $Q=14$. Это возможно, пока $14\ge \frac{L}{20}$, то есть $L\le 280$.
Что же будет происходить при 280
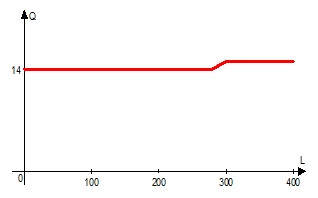
$$ Q^*(L)=\begin{cases}
14, & L \le 280\\
\frac{L}{20}, & 280 < L < 300\\
15, & L \ge 300
\end{cases} $$
4. Уборка в общежитии
Каждый из студентов хотел бы, чтобы комната была чистой, однако оба не любят убираться, причем Алексей не любит уборку вдвое сильнее, чем Михаил. Это отражено в их функциях полезности: полезность Михаила равна $G⋅(8-x_m)$, а полезность Алексея имеет вид $G⋅(8-2x_a)$.
Расписание устроено так, что по субботам в первой половине дня в комнате отсутствует Алексей, а во второй — Михаил. Когда Алексей приходит с учебы, он видит «промежуточную» степень чистоты комнаты (равную уровню усилий Михаила) и принимает решение о том, сколько усилий приложить для завершения уборки.
а) Каковы будут уровни усилий, которые будут прикладывать Алексей и Михаил к уборке? Каков будет итоговый уровень чистоты комнаты?
б) Могут ли ребята договориться об уровнях усилий так, чтобы обоим стало лучше по сравнению с результатом пункта а)? Верно ли, что при этом комната непременно будет чище, чем в пункте а)?
Полезность Алексея имеет вид: $U_a=(x_a+x_m )(8-2x_a)$. Относительно выбираемой переменной $x_a$ это парабола с ветвями вниз, она имеет вершину в точке $x_a^*=(4-x_m)/2 (при x_m<4)$. (4 балла)
Подставляя это в полезность Михаила, получаем: $U_m=((4-x_m)/2+x_m )(8-x_m)$ . Это также парабола с ветвями вниз, она имеет вершину в точке $x_m^*=2$. Получаем, что $x_a^*=1$, $G^*=3$. (4 балла)
(б) (8 баллов) Полезности обоих ребят в а) равны 18. Легко привести примеры уровней усилий такие, что полезности обоих больше, чем 18. Например, если каждый будет убираться немного больше (скажем, $x_m^*=3, \ x_a^*=2$), то полезность Михаила вырастет до 25, а полезность Алексея – до 20. (4 балла за любой пример) Комната при этом будет чище.
Можно ли привести пример такой пары уровней усилий, что обоим лучше по сравнению с а), но комната оказывается грязнее, чем в а)? Докажем, что сделать этого нельзя.
Имеем систему
$$\begin{cases}
U_m=(x_a+x_m )(8-x_m)>18\\
U_a=(x_a+x_m )(8-2x_m)>18
\end{cases}$$
Если при каких-то уровнях усилий $x_m^*, x_a^*$ полезность Алексея оказалась больше, чем 18, то максимальная полезность Алексея при уровне усилий Михаила, равном $x_m^*$, и подавно должна оказаться больше 18. Подставляя функцию наилучшего ответа Алексея $x_a=\frac{(4-x_m)}{2}$, в его полезность, получаем, что максимально достижимая полезность Алексея равна $U_a^\max=\frac{(4+x_m)^2}{2}$.
Поэтому из второго уравнения системы следует, что $\frac{(4+x_m)^2}{2}>18$, откуда $x_m^*>2$.
Это означает, что в левой части первого уравнении системы второй сомножитель меньше 6. Поскольку произведение должно оказаться больше 18, первый сомножитель (чистота комнаты) должен быть больше 3, что и означает, что комната должна оказаться чище, чем в (а).
Итак, обоим может стать лучше только в случае, если комната окажется чище. (4 балла)
5. Кредит самому себе
2. Даже если такой кредит получить удастся, после покупки банка нельзя будет «разрешить себе» его не возвращать: кредит будет выдан из каких-то пассивов банка (например, депозитов, размещенных в нем), которые придется возвращать вкладчикам.