1. Я больше не буду играть в эту игру
Маги в Шогилу продает фирма-монополист «Голлы Ралександра», его функция издержек задается как $TC = 6q$. Фирма максимизирует свою прибыль. При этом монополист может выбрать заплатить $\alpha^2$ денежных единиц загадочной подруге Элли – Йонмель, которая в таком случае будет готова приобрести $\alpha$ единиц Магов в Шогилу по той же цене, что и Элли. Если Элли приобретет $0$ единиц товара, Йонмель не купит ничего и обиженно уйдет вместе с подругой.
- (10 баллов) Выведите рыночный спрос в зависимости от $\alpha$.
- (15 баллов) Определите значение $\alpha$, которое выберет монополист, и найдите прибыль, которую он получит.
- (5 баллов) Предположим теперь, что деятельностью «Голлы Ралександра» недоволен верховный орган правительства – Суд Фортуны. Через особые каналы воздействия Суд Фортуны добился того, что издержки монополиста возросли до $TC = 10q$, а плата, которую необходимо отдавать Йонмель возрасла до $5\alpha^2 + 6$. Определите новое равновесное значение $\alpha$ и прибыль монополиста.
- Бюджетное ограничение Элли: $pq \leqslant 20$ или $q \leqslant \frac{20}{p}$.
Промаксимизируем полезность:
$$U = -q^2 + (42 - 2p)q \rightarrow \underset{q \geqslant 0}{max}$$
$$q^* = \frac{42 - 2p}{2} = 21 - p$$
Очевидно, что количество товара не может быть отрицательным, поэтому $p \leqslant 21$.Проверим, при каких значениях цены выполняется бюджетное ограничение:
$$21 - p \leqslant \frac{20}{p} \Rightarrow p^2 - 21p + 20 \geqslant 0 \Rightarrow (p - 20)(p - 1) \geqslant 0$$
$$\left[
\begin{gathered}
0 \leqslant p \leqslant 1
\\
20 \leqslant p \leqslant 21
\end{gathered}
\right.$$
Если бюджетное ограничение не выполняется, значит Элли тратит больше денег, чем имеет, поэтому в этом случае оптимальное потребление Магов в Шогилу будет равно $\frac{20}{p}$, т.е. она просто потратит весь свой доход.Так, можем записать спрос Элли на Маги в Шогилу:
$$q^d =
\begin{cases}
21 - P,& 0 \leqslant P \leqslant 1
\\
\frac{20}{P},& 1 < P < 20
\\
21 - P,& 20 \leqslant P \leqslant 21
\\
0,& P > 21
\end{cases}
$$
Теперь добавим к спросу Элли спрос её подруги Йонмель и получим рыночный спрос на Маги в Шогилу в зависимости от $\alpha$:
$$Q^d =
\begin{cases}
21 + \alpha - P,& 0 \leqslant P \leqslant 1
\\
\frac{20}{P} + \alpha,& 1 < P < 20
\\
21 + \alpha - P,& 20 \leqslant P < 21
\\
0,& P \geqslant 21
\end{cases}
$$ - Рассмотрим 4 случая, в каждом из которых будем максимизировать прибыль монополиста.
- $Q^d = 21 - P,~ P \in [0, 1] \cup [20, 21]$
$$\Pi_1 = 21P - P^2 - 126 + 6P = -P^2 +27P-126$$
Функция прибыли имеет вид параболы ветвями вниз, поэтому максимум – в вершине.
$$P^* = \frac{27}{2} = 13,5 \notin [0, 1] \cup [20, 21]$$
Видно, что найденная цена не принадлежит нужному промежутку, поэтому выбираем ближайшее значение из промежутка (поскольку имеем дело с параболой ветвями вниз, чем дальше мы от вершины, тем меньше значение функции). Значит $P^* = 20 \Rightarrow \Pi_1 = -400 + 540 - 126 = 14$. - $Q^d = \frac{20}{P},~ P \in [1, 20]$
$$\Pi_2 = 20 - \frac{120}{P}$$
$$\Pi'_2 = \frac{120}{P^2} > 0 \forall P$$
Получили, что производная всегда положительна, значит функция всегда возрастает, поэтому выбираем наибольшее возможное значение цены: $P^* = 20 \Rightarrow \Pi_2 = 20 - 6 = 14$. - $Q^d = 21 + \alpha - P,~ P \in [0, 1] \cup [20, 21]$
$$\Pi_3 = 21P + \alpha P - P^2 - 126 - 6\alpha + 6P - \alpha^2 = -P^2 + (27 + \alpha)P - 126 - 6\alpha - \alpha^2$$
функция прибыли имеет вид параболы ветвями вниз по $P$, поэтому максимум – в вершине.
$$P^* = \frac{27 + \alpha}{2} \Rightarrow \alpha \in [13, 15]$$
Подставим найденное значение цены в прибыль и промаксимизируем по $\alpha$:
$$\Pi_3 = \frac{(27 + \alpha)^2}{4} - 126 - 6\alpha - \alpha^2 = -0,75\alpha^2 + 7,5\alpha + 56,25$$
Функция прибыли имеет вид параболы с ветвями вниз, поэтому максимум – в вершине.
$$\alpha^* = 5 \notin [13, 15]$$
Найденное оптимальное значение не принадлежит промежутку, поэтому будем брать ближайшее допустимое, т.е. $\alpha^* = 13 \Rightarrow \Pi_3 = -0,75\cdot 169 + 7,5 \cdot 13 + 56,25 = 27$. - $Q^d = \frac{20}{P} + \alpha,~ P \in [1, 20]$
$$\Pi_4 = 20 + \alpha P - \frac{120}{P} - 6\alpha - \alpha^2 = -\alpha^2 + (P - 6)\alpha + 20 - \frac{120}{P}$$
Функция прибыли имеет вид параболы ветвями вниз относительно $\alpha$, поэтому максимум – в вершине.
$$\alpha^* = \frac{P - 6}{2}$$
Подставим полученное значение обратно в прибыль:
$$\Pi_4 = \frac{(P - 6)^2}{4} + 20 - \frac{120}{P}$$
$$\Pi'_4 = \frac{P - 6}{2} + \frac{120}{P^2} > 0~ \text{при допустимых} ~a$$
Получили, что производная всегда положительна на ограничении, значит будем выбирать наибольшее возможное $P^* = 20 \Rightarrow \Pi_4 = 49 + 20 - 6 = 63$.
Таким образом, наибольшее значение прибыли получили в четвёртом случае. В этом случае монополист выбирает $P^* = 20$, а значит $\alpha = \frac{20 - 6}{2} = 6$, а прибыль равна 63.
- $Q^d = 21 - P,~ P \in [0, 1] \cup [20, 21]$
- Точно так же, как и в предыдущем пункте рассмотрим 4 случая.
- $Q^d = 21 - P,~ P \in [0, 1] \cup [20, 21]$
$$\Pi_1 = 21P - P^2 - 210 + 10P = -P^2 + 31P - 210$$
Функция прибыли имеет вид параболы ветвями вниз, значит максимум – в вершине.
$$P^* = \frac{31}{2} = 15,5 \notin [0, 1] \cup [20, 21]$$
Найденное оптимальное значение не принадлежит допустимому промежутку, поэтому выбираем ближайшее: $P^* = 20 \Rightarrow \Pi_1 = -400 + 620 - 210 = 10.$ - $Q^d = \frac{20}{P},~ P \in [1, 20]$
$$\Pi_2 = 20 - \frac{200}{P}$$
$$\Pi'_2 = \frac{200}{P^2} > 0$$
Получили, что производная всегда положительна, значит функция всегда возрастает, поэтому выбираем наибольшее возможное $P^* = 20 \Rightarrow \Pi_2 = 20 - 10 = 10$. - $Q^d = 21 + \alpha - P,~ P \in [0, 1] \cup [20, 21]$
$$\Pi_3 = (21 - P)P + \alpha P - 10(21 - P) - 10\alpha - 5\alpha^2 - 6 = -5\alpha^2 + (P - 10)\alpha + (21 - P)(P - 10) - 6$$
Функция прибыли имеет вид параболы ветвями вниз, поэтому максимум – в вершине.
$$P^* = \frac{P - 10}{10}$$
Подставим найденное значение цены обратно в прибыль:
$$\Pi_3 = \frac{(P - 10)^2}{20} - (P - 21)(P - 10) - 6$$
$$\Pi'_3 = \frac{P - 10}{10} - P + 10 - P + 21 - 6 = 0$$
$$P^* = \frac{240}{19} \notin [0, 1] \cup [20, 21]$$
Найденное оптимальное значение не принадлежит оптимальному промежутку, выбираем ближайшее: $P^* = 20 \Rightarrow \Pi_3 = 5 + 10 - 6 = 9$. - $Q^d = \frac{20}{P} + \alpha,~ P \in [1, 20]$
$$\Pi_4 = 20 + \alpha P - \frac{200}{P} - 10\alpha - 5\alpha^2 - 6 = -5\alpha^2 + (P - 10)\alpha + 14 - \frac{200}{P}$$
Функция прибыли имеет вид параболы ветвями вниз относительно $\alpha$, значит максимум – в вершине.
$$\alpha^* = \frac{P - 10}{10}$$
Подставим найденное значение обратно в прибыль:
$$\Pi_4 = \frac{(P - 10)^2}{20} - \frac{200}{P} + 14$$
$$\Pi'_4 = \frac{P - 10}{10} + \frac{200}{P^2} > 0$$
Получили, что производная положительна для всех допустимых $P$, значит функция все время возрастает, поэтому выбираем наибольшее возможное $P^* = 20 \Rightarrow \Pi_4 = 5 - 10 + 14 = 9$.
Получили, что наибольшая прибыль монополиста при новых условиях равна $10$ и достигается в условиях отсутствия торговли с Йонмель, т.е. при $\alpha = 0$.
- $Q^d = 21 - P,~ P \in [0, 1] \cup [20, 21]$
2. Сезонный продукт
- (5 баллов) Определите изначальные равновесные цену и количество на рынке пирожков с голубикой зимой и летом до появления новой технологии.
- (3 балла) Какие цена и количество складывались бы на рынке летом, если бы государство не запрещало новую технологию?
- (15 баллов) Определите оптимальное значение $a$, если государство хочет максимизировать общественное благосостояние, которое включает в себя благосостояние потребителей, производителей и самого государства.
- (7 баллов) Получится ли у государства достичь того же уровня общественного благосостояния, как в случае, если бы оно не запрещало новую технологию выращивания голубики?
- Зимой спрос задаётся функцией $Q^d = 100 - P$, а предложение: $Q^s = 3P$. Равновесию соответствует точка пересечения кривых спроса и предложение. Аналитически нам нужно просто приравнять их уравнения: $100 - P = 3P \Rightarrow P^*_w = 25,~ Q^*_w = 100 - 25 = 75$.
Летом спрос задаётся функцией $Q^d = 100 - P$, а предложение до появления новой технологии имеет вид $Q^s = P$. Тогда равновесие: $100 - P = P \Rightarrow P^*_{s_1} = 50,~ Q^*_{s_1} = 50$.
- С появлением новой технологии до вмешательства государства предложение имело вид: $Q^s = 2P$. Тогда равновесие: $100 - P = 2P \Rightarrow P^*_{s_2} = \frac{100}{3},~ Q^*_{s_2} = \frac{200}{3}$.
-
- Первый вариант решения:
Условие можно было понять так, что государство своими закупками увеличивает спрос на $2a$ при каждом значении цены. Тогда спрос будет иметь вид $Q^d = 100 + 2a - P$, а предложение – $Q^s = P$. Равновесие на этом рынке: $100 + 2a - P = P \Rightarrow P^* = 50 + a,~ Q^* = 50 + a$. Изобразим спрос и предложение на графике:
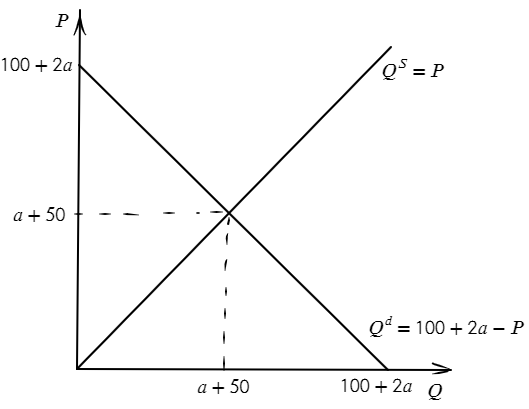
Общественное благосостояние – это сумма излишка потребителей, излишка производителей и излишка государства. Графически излишек потребителей – это площадь треугольника, ограниченного кривой спроса и прямой, соответствующей равновесной цене, а излишек производителей – площадь треугольника, ограниченного кривой предложения и прямой, соответствующей равновесной цене. Излишек государства в данном случае это просто его расходы, то есть $-a^2$. Таким образом, общественное благосостояние имеет вид: $SW = 0,5 \cdot (a + 50)(2a + 100 - a - 50) + 0,5 \cdot (a + 50)(a + 50) -a^2 = a^2 + 100a + 2500 - a^2 = 100a + 2500$. Видно, что общественное благосостояние возрастает по $a$, а значит, если государство старается максимизировать общественное благосостояние, то будет выбирать как можно большее значение $a$. Поскольку $a$ никак не ограничено, оптимальный выбор государства: $a \rightarrow +\infty$.
- Второй вариант решения:
На самом деле государство не может увеличить спрос на константу при любом значении цены. Если цена поднимется выше максимальной цены, которую готовы платить потребители (в нашем случае это $100$), то спрос будет предъявлять только государство на уровне $2a$, т.е. при $P > 100$ мы будет иметь вертикальный участок спроса $Q = 2a$. При этом равновесие у нас будут при: $100 + 2a - P = P \Rightarrow P^* = a+50,~ Q^* = a + 50$.
В этом случае общественное благосостояние – это всё ещё сумма излишка потребителей, излишка производителей и излишка государства, однако графически они будут считаться немного иначе. Изобразим спрос и предложение на графике:
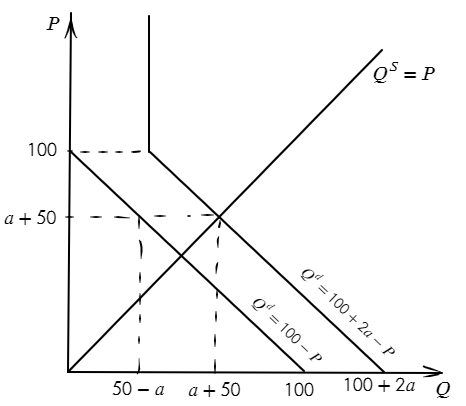
Излишек производителей графически – это площадь треугольника, ограниченного кривой предложения и прямой, соответствующей равновесной цене, а излишек потребителей – это площадь треугольника, ограниченного кривой спроса (только участком, соответствующим самим потребителям, а не государству и потребителям) и прямой, соответствующей равновесной цене. Для удобства заштрихуем эти фигуры на графике:
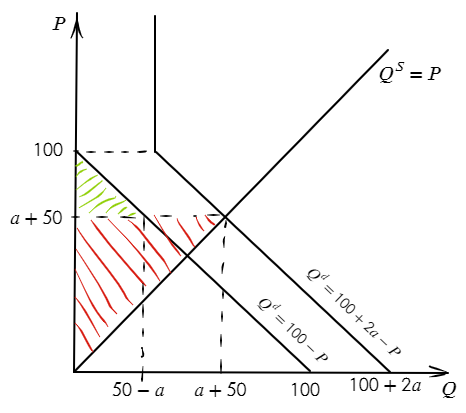
Зелёным цветом заштрихован треугольник, соответствующий излишку потребителей, красным цветом – треугольник, соответствующий излишку производителей. Излишек государства составляет $-a^2$.
Таким образом, общественное благосостояние имеет вид: $SW = 0,5 \cdot (50 - a)(100 - a - 50) + 0,5 \cdot (a + 50)(a + 50) - a^2 = 2500$. В этом случае общественное благосостояние постоянно и равно $2500$.
Однако, если государство закупит достаточно много пирожков с голубикой, цена вырастет настолько, что потребители больше не будут покупать этот товар. Графически эта ситуация выглядит так:
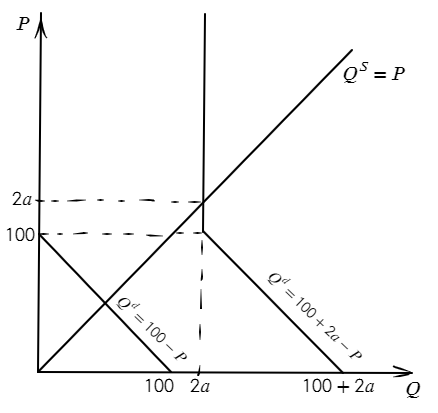
Произойдёт это в том случае, если закупки государства, то есть $2a$ превысят $100$, т.е. при $a > 50$. В этом случае равновесие складывается при $P^* = 2a,~ Q^* = 2a$. Излишек потребителей в этом случае равен $0$, поскольку они не покупают пирожки с голубкой совсем, а излишек производителей будет равен $0,5 \cdot 2a \cdot 2a = 2a^2$. Тогда общественное благосостояние имеет вид: $SW = 2a^2 - a^2 = a^2$. Видно, что при любом положительном $a$ общественное благосостояние бесконечно возрастает с ростом $a$. Поскольку государство стремится сделать общественное благосостояние как можно выше, оно выберет бесконечно большое $a$ и, соответственно, бесконечно большое общественное благосостояние.
- Первый вариант решения:
- Если бы государство не запрещало новую технологию, то общественное благосостояние составило бы: $SW = 0,5\cdot \frac{200}{3}(100 - \frac{100}{3}) + 0,5\cdot \frac{200}{3} \cdot \frac{100}{3} = \frac{10000}{3}$. В случае запрета технологии, но наличия государственных закупок, общественное благосостояние стремится к бесконечности. Таким образом, государству удалось значительно увеличить общественное благосостояние.
3. Организаторы организуют
мерча, а $y$ – количество экспериментов.
- (12 баллов) Найдите, сколько единиц мерча и экспериментов будет потреблять Миша и проиллюстрируйте ваше решение на графике (начертите карту кривых безразличия и покажите выбор оптимальной точки).
- (8 баллов) Пусть про удивительные товары (эксперименты и мерч) узнал Антон и стал потреблять эти товары вместо Мишы. Его функция полезности задаётся уравнением: $U=-x^2+8,5x+y$. Сколько мерча и экспериментов потребит Антон?
- (10 баллов) Выведите функцию спроса Антона на мерч (в зависимости от цены на мерч), если цена эксперимента равна $1$ тыс. руб.
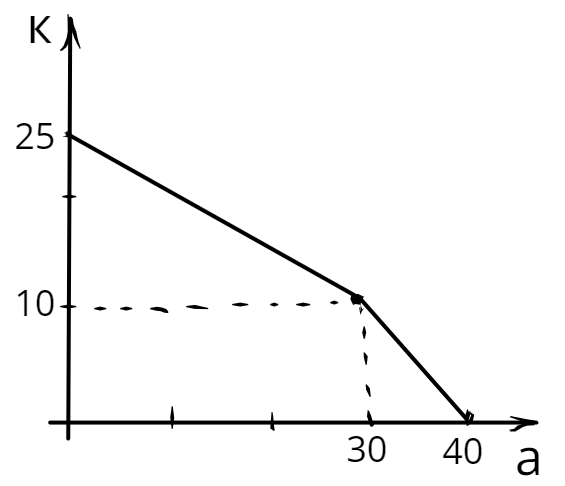
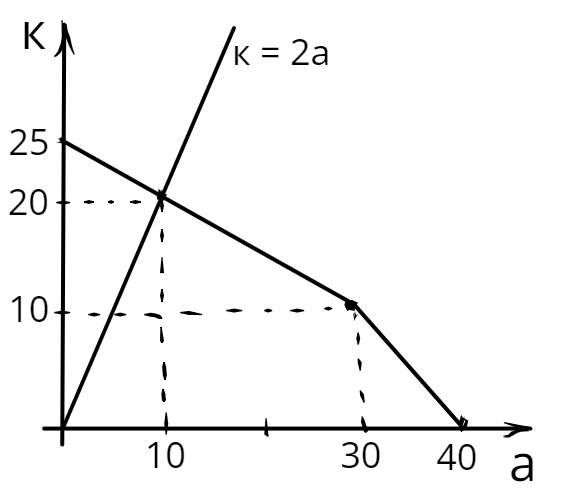
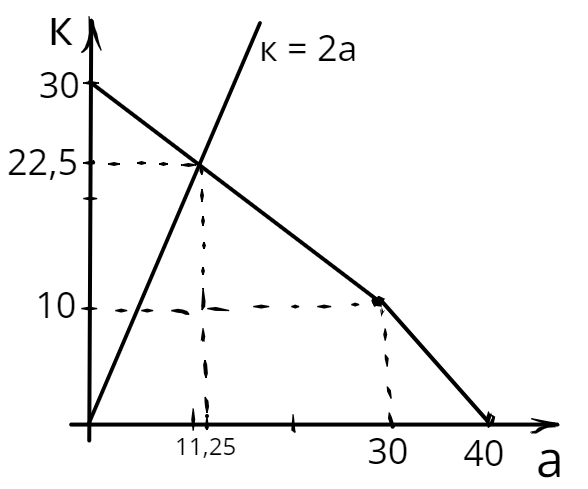
- Альтернативная стоимость производства экспериментов для Кирилла: $AC^K_e = 2$, альтернативная стоимость производства экспериментов для Гоши: $AC^G_e = 0,25$. Суммарно Кирилл и Гоша могут произвести $100$ экспериментов или $60$ единиц мерча. Построим кривую производственных возможностей Гоши и Кирилла, руководствуясь тем, что альтернативная стоимость производства растёт с ростом объёмов производства.
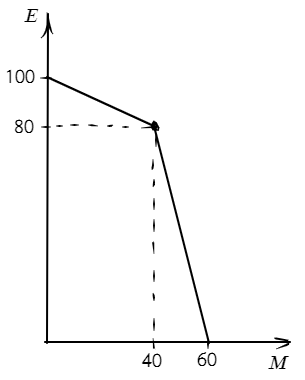
Функция полезности Миши $U = min{x, y}$. Такая функция полезности соответствует комплементарным товарам, кривые безразличия имеют вид «уголков», вершины которых располагаются на прямой $y = x$. Оптимальной точкой будет являться точка, в которой пересекаются КПВ Гоши и Кирилла и кривая безразличия Миши. Искомой кривой безразличия в данном случае будет являться та, которая имеет ровно одну точку пересечения с КПВ. Изобразим карту кривых безразличия, КПВ и оптимальную точку на одном графике:
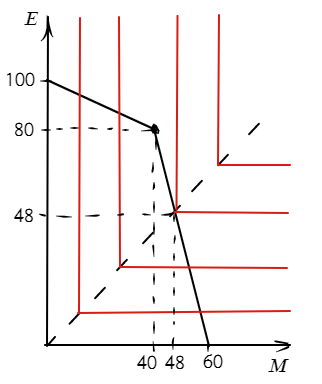
Видно, что оптимальная точка находится на втором (слева-направо) участке КПВ. Уравнение этого участка: $y = 240 - 4x$. Приравняем уравнение второго участка КПВ и прямой $y = x$: $240 - 4x = x \Rightarrow x^* = 48,~ y^* = 48$. Таким образом, в оптимуме будет потребляться по $48$ единиц мерча и экспериментов.
- Здесь стоит рассмотреть два случая.
- Первый случай: оптимум находится на первом (слева-направо) участке КПВ.
Уравнение первого участка КПВ: $y = 100 - 0,5x,~ x \in [0, 40]$. Подставим это в полезность Антона и промаксимизируем её.
$$U_1 = -x^2 + 8,5x + 100 - 0,5x = -x^2 + 8x + 100 \rightarrow \underset{x \in [0, 40]}{max}$$
Функция полезности имеет вид параболы ветвями вниз, поэтому максимум – в вершине.
$$x^* = \frac{8}{2} = 4 \in [0, 40],~ y^* = 98$$
$$U_1^* = -16 + 32 + 100 = 116$$ - Второй случай: оптимум находится на втором (слева-направо) участке КПВ.
Уравнение второго участка КПВ: $y = 240 - 4x,~ x \in [40, 60]$. Подставим это в полезность Антона и промаксимизируем её.
$$U_2 = -x^2 + 8,5x + 240 - 4x = -x^2 + 4,5x + 240 \rightarrow \underset{x \in [40, 60]}{max}$$
Функция полезности имеет вид параболы ветвями вниз, поэтому максимум – в вершине.
$$x_{\text{в}} = \frac{4,5}{2} = 2,25 \notin [40, 60]$$
Видно, что вершина параболы не принадлежит промежутку, значит выбираем граничную точку промежутку, ближайшую к координате вершине, это – $x = 40$, тогда найдём полезность:
$$U_2^* = -1600 + 180 + 240 = -1180$$
Во втором случае полезность, очевидно, меньше, чем в первом, значит оптимальные объёмы потребления мерча и экспериментов найдены в первом случае.
- Первый случай: оптимум находится на первом (слева-направо) участке КПВ.
- Запишем бюджетное ограничение Антона в общем виде:
$P_x \cdot x + P_y \cdot y \leqslant I$, где $P_x,~ P_y$ – цены мерча и экспериментов соответственное, а $I$ – доход Антона. С учётом данных из условия можем переписать бюджетное ограничение Антона в следующем виде: $P_x \cdot x + y \leqslant I$ или $y \leqslant I - P_x \cdot x$. Заметим, что если $y < I - P_x \cdot x$, мы может немного увеличить $y$ и уменьшить $x$, при этом увеличив полезность, поэтому неравенство можно заменить на равенство. Тогда подставим бюджетное ограничение в полезность Антона и промаксимизируем:
$$U = -x^2 + 8,5x + I - P_x \cdot x = -x^2 + (8,5 - P_x)x + I \rightarrow \underset{0 \leqslant x \leqslant \frac{I}{P_x}}{max}$$
Функция полезности имеет вид параболы ветвями вниз, поэтому максимум – в вершине.
$$x^* = \frac{8,5 - P_x}{2}$$
Заметим, что если $P_x > 8,5$, то товар $x$ становится слишком дорогим, и Антон перестаёт его покупать, т.е. $x^* = 0,~ P_x > 8,5$. С другой стороны, если расходы на товар $x$ в оптимуме превышают доход Антона, то он будет потреблять ровно $x^* = \frac{I}{P_x},~ \frac{8,5 - P_x}{2} > \frac{I}{P_x}$.Таким образом, спрос на мерч состоит из трёх участков:
$$x^d =
\begin{cases}
0,& P_x > 8,5
\\
\frac{8,5 - P_x}{2},& P_x \leqslant 8,5,~ \frac{8,5 - P_x}{2} \leqslant \frac{I}{P_x}
\\
\frac{I}{P_x},& \frac{8,5 - P_x}{2} > \frac{I}{P_x}
\end{cases}
$$
4. Eco-friendly
- (10 баллов) «Pirelli» является монополистом на рынке покрышек в городе Врн. Определите, какое $\beta$ выберет фирма, какой объем продукции произведет и какую прибыль получит.
- (2 балла) Какой размер аккордной субсидии должно выплатить фирме государство, чтобы производство стало экологичным? Считайте, что если фирме безразлично, делать заводы экологичными или нет, она будет делать первое. Государство выплачивает субсидию только тем фирмам, которые заботятся об экологии!
- (18 баллов) Теперь правительство региона взяло «Pirelli» под свой контроль и само выбирает коэффициент $\beta$. Оно руководствуется интересами общества и максимизирует совокупную функцию полезности $U=\sqrt{\beta}+\pi$, где $\pi$ – прибыль фирмы. Взаимодействие между государством и компанией устроено так: сначала государство выбирает значение $\beta$, а затем фирма выбирает объем производства. Какое значение $\beta$ установит государство?
- Запишем обратную функцию спроса: $P^d = 100 + 20\beta - Q$. Теперь можем записать функцию прибыли монополиста:
$$\Pi = (100 + 20\beta)Q - Q^2 - (1 + \beta)Q^2 - 100 - 50\beta = -(2 + \beta)Q^2 + (100 + 20\beta)Q - 100 - 50\beta \rightarrow \underset{Q \geqslant 0}{max}$$
Функция прибыли имеет вид параболы ветвями вниз относительно $Q$, поэтому максимум – в вершине.
$$Q^* = \frac{100 + 20\beta}{2(2 + \beta)}$$
Подставим найденное оптимальное количество обратно в прибыль:
$$\Pi = -\frac{(2 + \beta)(100 + 20\beta)^2}{4(2 + \beta)^2} + \frac{(100 + 20\beta)^2}{2(2 + \beta)} - 100 - 50\beta = \frac{(100 + 20\beta)^2}{4(2 + \beta)} - 100 - 50\beta$$
Сравним прибыли при $\beta = 0$ и $\beta = 1$:
$$\Pi(\beta = 0) = \frac{100 \cdot 100}{4\cdot 2} - 100 = 1250 - 100 = 1150$$
$$\Pi(\beta = 1) = \frac{120 \cdot 120}{4\cdot 3} -100 - 50 = 1200 - 150 = 1050$$
Очевидно, $\Pi(\beta = 0) > \Pi(\beta = 1) \Rightarrow \beta^* = 0,~ \Pi^* = 1150,~ Q^* = \frac{100}{4} = 25$. - Аккордная субсидия просто прибавляется к прибыли, как константа. Для того, чтобы фирме было выгодно выбрать экологичное производство, должно выполняться неравенство: $\Pi(\beta = 0) \leqslant \Pi(\beta = 1) + S$, где $S$ – размер субсидии. Подставив числа из предыдущего пункта, получим:
$$1150 \leqslant 1050 + S \Rightarrow S \geqslant
100$$ - Оптимальный выбор объёма производства в зависимости от $\beta$ не изменится, поэтому прибыль в зависимости от $\beta$ имеет вид: $\Pi = \frac{(100 + 20\beta)^2}{4(2 + \beta)} - 100 - 50\beta$. Тогда совокупная функция полезности имеет вид:
$$U = \sqrt{\beta} + \frac{(100 + 20\beta)^2}{4(2 + \beta)} - 100 - 50\beta$$
Сравним полезности при $\beta = 0$ и $\beta = 1$:
$$U(\beta = 0) = \frac{100\cdot 100}{4\cdot 2} - 100 = 1150$$
$$U(\beta = 1) = 1 + \frac{120\cdot 120}{4\cdot 3} - 100 - 50 = 1051$$
Видно, что $U(\beta = 0) > U(\beta = 1)$, поэтому государство выберет $\beta^* = 0$