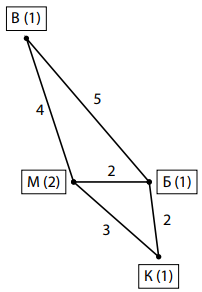
1. Сосисочная олигополия
а) (3 балла) Во главе фирмы A стоит некомпетентный директор, который не имеет понятия, как нужно выбирать выпуск, чтобы получить максимальную прибыль, и просто выбирает произвольный объем выпуска $q_A$. Какой объем выпуска $q_B$ выберет фирма B в ответ, если она прекрасно умеет максимизировать прибыль?
б) (3 балла) Предположим, фирму A возглавил более компетентный менеджер, который умеет выбирать выпуск так, чтобы в результате его фирма получила максимальную прибыль. Какой объем выпуска он выберет?
2. Бесконечные апелляции
В таблице приведена статистика о ходе судебных процессов по искам физических лиц в Кукумбрии в 2017 году. «Участниками» называются стороны, чей спор рассматривается в суде.
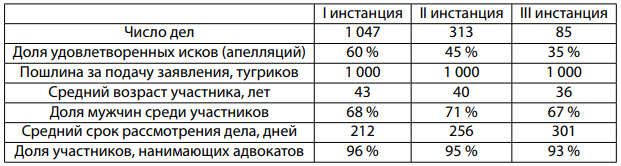
Казалось бы, оптимальной стратегией каждой стороны, недовольной судебным решением, было бы обжалование решения подряд во всех инстанциях. В этом случае работа судов была бы парализована.
а) (3 балла) Объясните, какой экономический механизм может препятствовать использованию такой стратегии? Иными словами, почему апелляции подают не все те, кто проигрывает в суде предыдущей инстанции?
б) (3 балла) Опыт проведения Всероссийских олимпиад по экономике показывает, что необоснованные апелляции на результаты проверки работ подает большое число участников. Пользуясь логикой предыдущего пункта, предложите механизм, который позволил бы жюри сократить число необоснованных апелляций. Имейте в виду, что должны сохраниться основные олимпиадные принципы, в том числе равноправие всех участников, стремление жюри исправить все неточности и обеспечить справедливые результаты. Объясните, почему вы считаете, что предложенный механизм должен сработать.
- Материальные издержки. В ходе судебного процесса возникают расходы на наём адвокатов и госпошлину.
- Издержки времени. Процесс рассмотрения апелляции занимает много времени. У потерянного времени есть альтернативная стоимость.
Если у проигравшей стороны нет достаточной уверенности в том, что решение является несправедливым, а шансы на положительный исход рассмотрения апелляции достаточно велики, то нет смысла подавать апелляцию — это с большой вероятностью обернется понесенными издержками при неизменном решении.
б) Например, можно предложить снимать 1 балл за заведомо необоснованную апелляцию. В этом случае число стратегических апелляций снизится, а подавать их будут школьники, уверенные в том, что при проверке была допущена ошибка
3. Мед и хлопья (8—9)
Молоко у жителей есть в неограниченном количестве, а мед и хлопья нужно производить. Каждый житель может тратить свое рабочее время на пасеке или в кукурузном поле. Будем считать, что один пасечник может следить за одним ульем пчел, который производит 1 литр меда. Урожай кукурузы зависит от интенсивности опыления пчелами. Некоторые пчелы летают в том числе на другой берег и опыляют кукурузу там, поэтому ежемесячный урожай кукурузы на каждом берегу зависит от того, сколько пчел на обоих берегах:
$$y_L = (b_L + b_R/3) \cdot x_L,$$
$$y_R = (b_R + b_L/3) \cdot x_R,$$
где $y$ – производство кукурузных хлопьев, $b$ – количество ульев пчел, $x$ – число рабочих, занятых в производстве кукурузных хлопьев (может быть нецелым). Индексы у всех переменных означают берег.
а) (3 балла) Пусть каждый регион независимо принимает решение о распределении труда между отраслями. Постройте графически кривую производственных возможностей каждого берега для какого-то фиксированного числа ульев на другом берегу. Назовем равновесием такое состояние, когда жители каждого берега не захотят менять распределение труда после того, когда узнают число ульев у другого берега. Сколько меда и хлопьев будет произведено в равновесии?
б) (3 балла) Предположим, два берега объединили усилия и совместно решают, как распределить трудовые ресурсы между пасеками и полями (при этом люди переплывать на другой берег не могут, но передавать мед и хлопья могут). Найдите общую границу производственных возможностей двух берегов. Найдите, сколько меда и хлопьев будет произведено в случае объединения усилий.
4. Коробки
Несмотря на то, что подарки сильно отличаются по весу, по размеру они примерно одинаковые. Подарки любых двух человек вместе помещаются в маленькую коробку, любых трех –– в среднюю (а в маленькую не помещаются), а всех четырех –– только в большую. Если какой-то набор подарков помещается в определенную коробку, то он помещается и в коробку большего размера.
Стоимость почтовых отправлений определяется по формулам нелинейного ценообразования. А именно, если кто-то хочет отправить посылку в маленькой коробке, то он должен заплатить 2000 рублей, а также по 1000 рублей за каждый килограмм веса содержимого коробки. Отправка посылки в средней коробке стоит 8000 рублей плюс 500 рублей за каждый килограмм содержимого. Отправка посылки в большой коробке стоит 18 500 рублей, но зато дополнительно ничего платить не нужно. Цена самой коробки в каждом случае включена в стоимость отправления.
Ребята думают, как им распределить посылки по коробкам и кто сколько должен заплатить. Распределение посылок и оплаты, которое их интересует, должно удовлетворять двум свойствам:
- эффективность: люди, которые упаковывают свои подарки в одну коробку, в сумме платят столько, сколько стоит отправка этой коробки;
- рациональность: никто из участников не платит больше, чем заплатил бы, если бы решил отправить посылку отдельно от остальных, а также нет такого набора участников, который мог бы упаковать свои подарки в одну коробку и заплатить меньше, чем платит при существующем распределении.
Предложите распределение, удовлетворяющее обоим свойствам, и докажите, что оно им удовлетворяет.