1. Доход или богатство
Государство намерено собрать с двух братьев 5 тугриков в виде налогов. Какую часть суммы заплатит каждый из них, зависит от того, что будет налогооблагаемой базой.
1. Предположим, налогом по ставке $х$% облагается только заработанная прибыль от проекта. Найдите $х$. Какую сумму заплатит каждый из братьев в виде налогов? Чему будет равна чистая прибыль от каждого из проектов после уплаты налогов? Как будут соотноситься между собой богатство Гриши и богатство Вани после уплаты налогов?
2. Предположим, налогом по ставке $y$% облагается совокупное богатство с учетом заработанного дохода. Найдите $y$. Какую сумму заплатит каждый из братьев? Чему будет равна чистая прибыль от каждого из проектов после уплаты налогов? Как будут соотноситься между собой богатство Гриши и богатство Вани после уплаты налогов?
3. Среди экономистов существует дискуссия о том, что нужно выбирать в качестве налогооблагаемой базы. В предыдущих пунктах задачи вы рассмотрели две альтернативы — налогообложение дохода и налогообложение богатства. Сравните эти альтернативы с точки зрения двух критериев:
а) В каком случае благосостояние перераспределяется от менее эффективных к более эффективным предпринимателям?
б) В каком случае неравенство по итоговому богатству выше?
Наконец, отношение богатства двух братьев составляет 115/100 = 1,15.
2) Поскольку налоговое бремя распределяется пропорционально объёму богатства каждого, Ваня заплатит в виде налогов 100/(100 + 120) * 5, то есть примерно 2,27 тугриков, Гриша —120/(100 + 120) * 5, то есть примерно 2,73 тугриков. После уплаты налогов чистая прибыль проекта Вани составит 0 – 2,27 = −2.27 тугриков, в то время как чистая прибыль проекта Гриши составит 0.2 * 100 – 2,73 = 17.27 тугриков. Наконец, отношение богатства двух братьев составляет (120 – 2,73)/(100 – 2,27) = 1.20.
3) а) В случае, когда налогом облагается богатство, а не доход, капитал перераспределяется от менее к более производительным проектам. Богатство Гриши в случае, когда налогом облагается налог, составляет 115, а когда налогом облагается богатство — 117,27.
б) С другой стороны, одним из потенциальных недостатков налогообложения богатства по сравнению с налогообложением дохода является увеличение неравенства по богатству (отношение выросло с 1.15 до 1.20).
2. Воспроизводимый ограниченный ресурс
Известно, что на первом предприятии для производства двух единиц товара Y нужно затратить одну единицу ресурса альфа и четыре единицы ресурса бета, а для производства единицы товара X потребуется только одна единица ресурса альфа.
На втором предприятии из единицы ресурса альфа и четырёх единиц ресурса бета можно получить одну единицу товара Y, а из единицы ресурса альфа можно произвести две единицы товара Х.
Также известно, что в процессе производства товара X образуется некоторое количество ресурса бета. Так на первом предприятии при производстве трёх единиц товара Xобразуются 4 единицы ресурса бета, а на втором предприятии при производстве трех единиц товара X образуются две единицы ресурса бета.
В начале каждого месяца город поставляет каждому предприятию 30 единиц ресурса альфа и 40 единиц ресурса бета, передавать и обменивать ресурсы предприятия не могут. Если на конец месяца у предприятия остаются ресурсы, то город их забирает. Т.е. в начале каждого месяца каждое предприятие имеет в своём распоряжении ровно 30 единиц ресурса альфа и ровно 40 единиц ресурса бета.
1. Постройте график КПВ каждого предприятия.
2. Предположим, в результате острой конкурентной борьбы произошло объединение этих двух предприятий в производственное объединение (ПО). Теперь ПО на тех же условиях получает от города каждый месяц 60 единиц ресурса альфа и 80 единиц ресурса бета. Постройте КПВ производственного объединения.
3. Пусть товар Y продается на рынке по цене 30, а товар X – по цене 10. Какой объём производства каждого товара позволит ПО получить наибольшую выручку и чему будет в этом случае равна выручка?
4. Как должна измениться цена товара Х, чтобы ПО изменило свой выбор относительно объемов производства товаров по сравнению с решением, принятым в п.3?
5. Предположим, что помимо товаров X и Yпроизводственное объединение может также продавать ресурс бета. Пусть цены на товары X и Y соответствуют пункту 3. При какой цене ресурса бета предприятие будет производить товар Y?
Предприятие 1:
$Y = min(2\alpha; \frac{1}{2}\beta$)
$X=\alpha$
$\beta^+=\frac{4}{3}X$
Предприятие 2:
$Y = min(\alpha; \frac{1}{4}\beta$)
$X=2\alpha$
$\beta^+=\frac{2}{3}X$
Заметим, что, если мы вставим в уравнения ресурсозатрат вместо $\alpha$ и $\beta$ количества данных ресурсов, которыми располагают предприятия, мы получим максимальное количество Y, которое могут произвести предприятия при нулевом производстве X (ведь ресурс $\alpha$, необходимый для производства X, мы полностью отправили на производство Y, как и ресурс $\beta$).
Но предприятия могут производить не только товар Y, часть ресурса $\alpha$ всё-таки идёт на производство товара X, следовательно, количество ресурса $\alpha$, задействованное в производстве Y уже будет меньше на эту самую часть.
И чем больше мы будем производить товара X, тем меньше ресурса α останется на производство товара Y.
Однако в процессе производства товара X выделяется ресурс $\beta$, который мы можем направить только на производства товара Y (что мы и сделаем). Отсюда следует, что чем больше мы производим товара X, тем больше ресурса $\beta$ мы можем задействовать на производстве товара Y.
Теперь выразим количества $\alpha$ и $\beta$, которые мы можем задействовать в производстве товара Y через объём производства товара X.
Предприятие 1:
$\alpha=30-X$
$\beta=40+\frac{4}{3}X$
Предприятие 2:
$\alpha=30-\frac{X}{2}$
$\beta=40+\frac{2}{3}X$
Теперь для того, чтобы получить уравнения КПВ нужно просто вставить количества α и β в уравнения ресурсозатрат производства товара Y.
Предприятие 1:
$Y=min(2(30-X); \frac{1}{2}(40+\frac{4}{3}X))=min(60-2X;20+\frac{2}{3}X)$
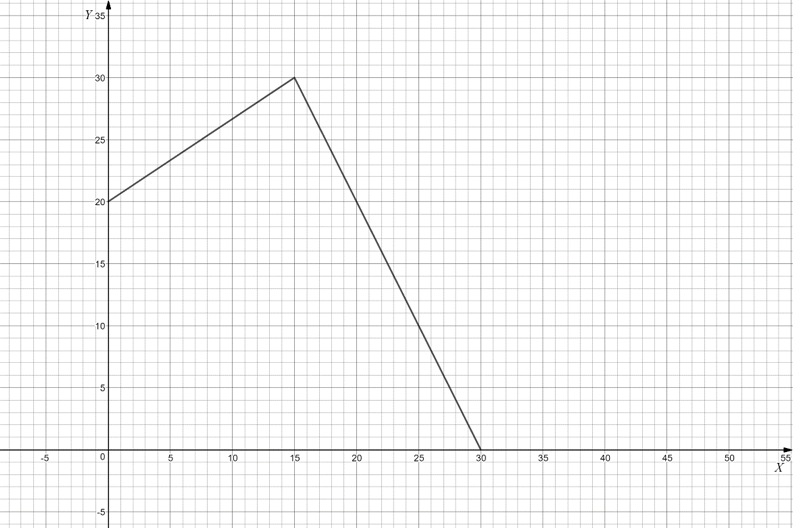
Предприятие 2:
$Y=min((30-\frac{X}{2}); \frac{1}{4}(40+\frac{2}{3}X))=min(30-\frac{X}{2};10+\frac{1}{6}X)$
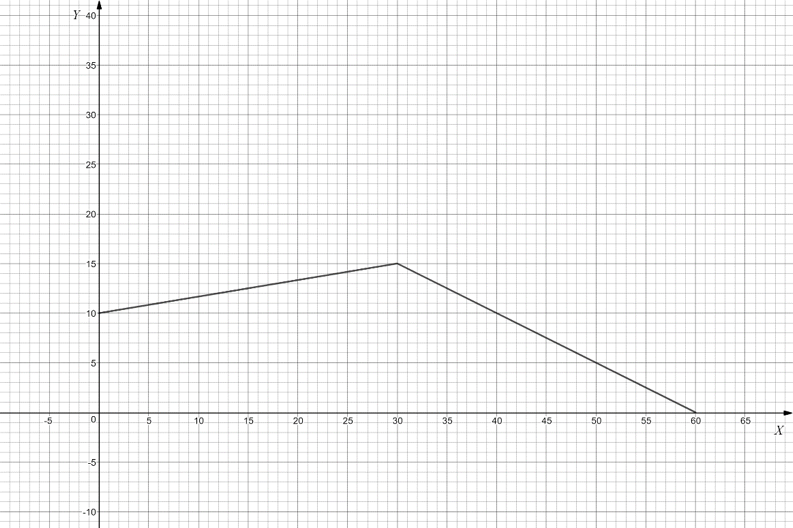
Ответ на второй вопрос
Из ответа на первый вопрос видно, что предприятие №1 должно специализироваться на производстве товара Y, а предприятие №2 на производстве товара X.
В таком случае уравнения ресурсозатрат ПО будут выглядеть так:
$Y = min(2\alpha; \frac{1}{2}\beta$)
$X=2\alpha$
$\beta^+=\frac{2}{3}X$
Чтобы получить уравнение КПВ выражаем ресурсы через X и подставляем значения в уравнение ресурсозатрат производства Y (т.е. делаем всё тоже самое, что и в предыдущем пункте, но не забываем, что кол-во доступных ресурсов теперь в два раза больше).
КПВ ПО
$Y=min(2(60-\frac{X}{2}); \frac{1}{2}(80+\frac{2}{3}X))=min(120-X;40+\frac{1}{3}X)$
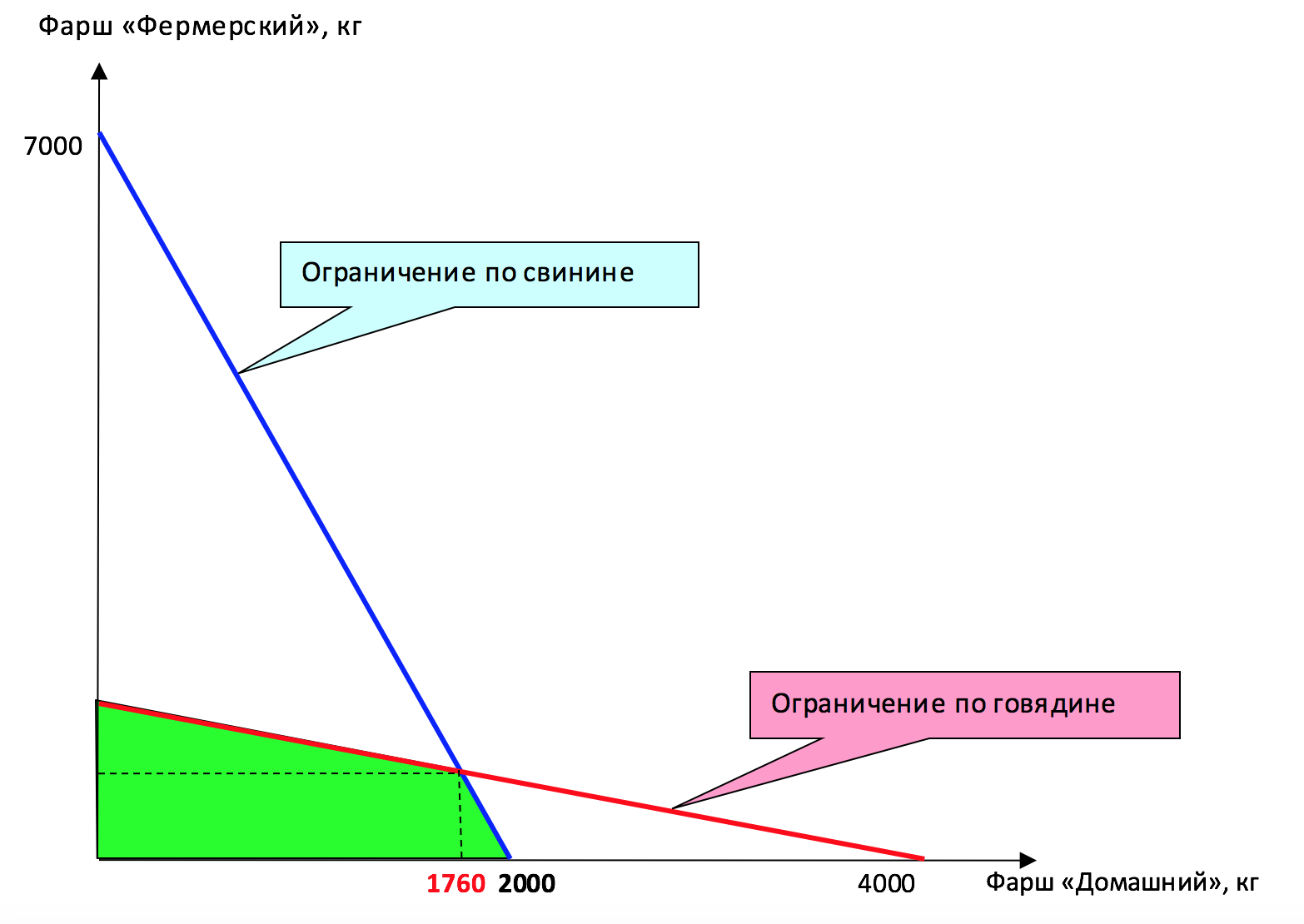
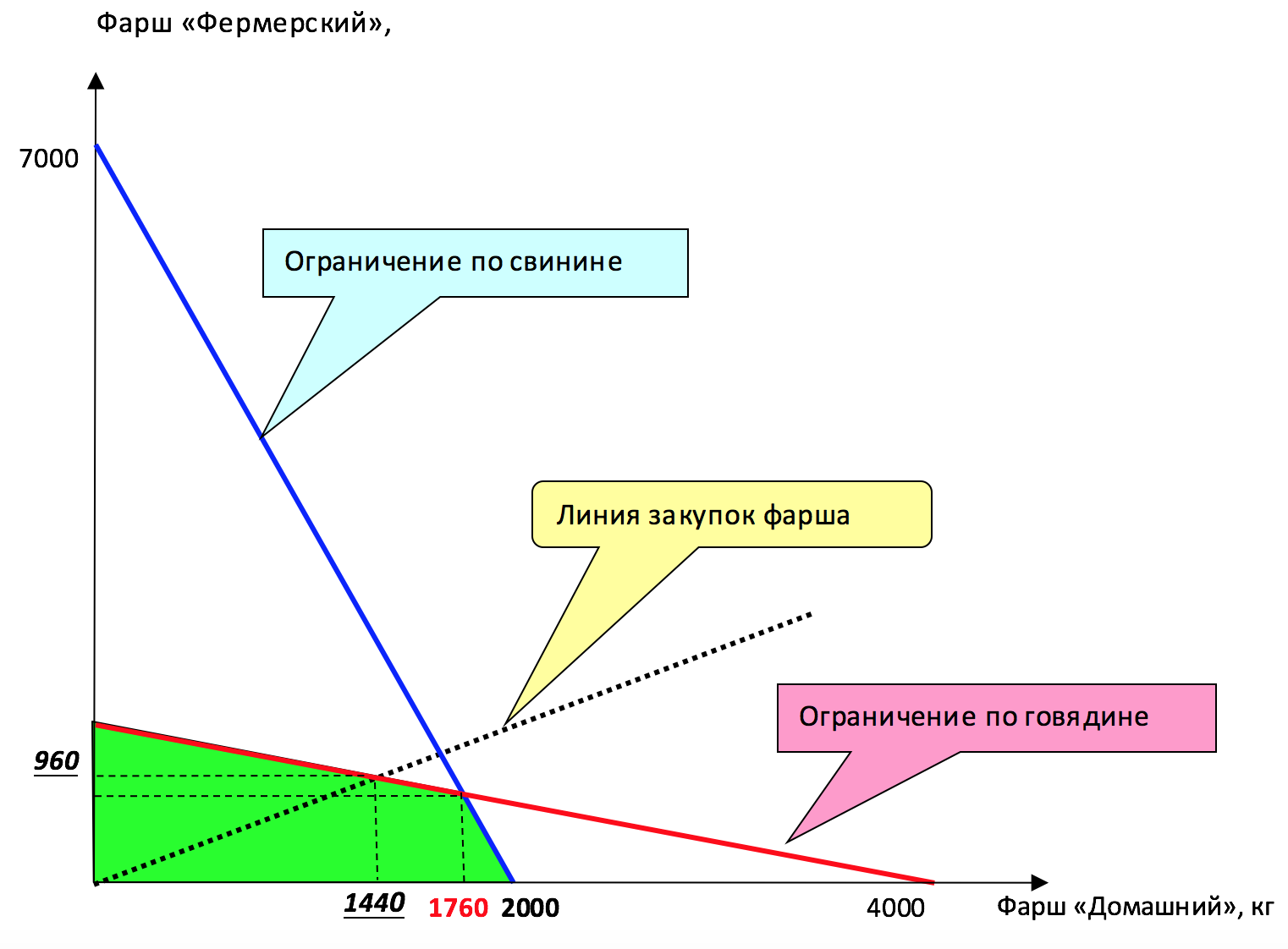
Ниже представлен график КПВ ПО.
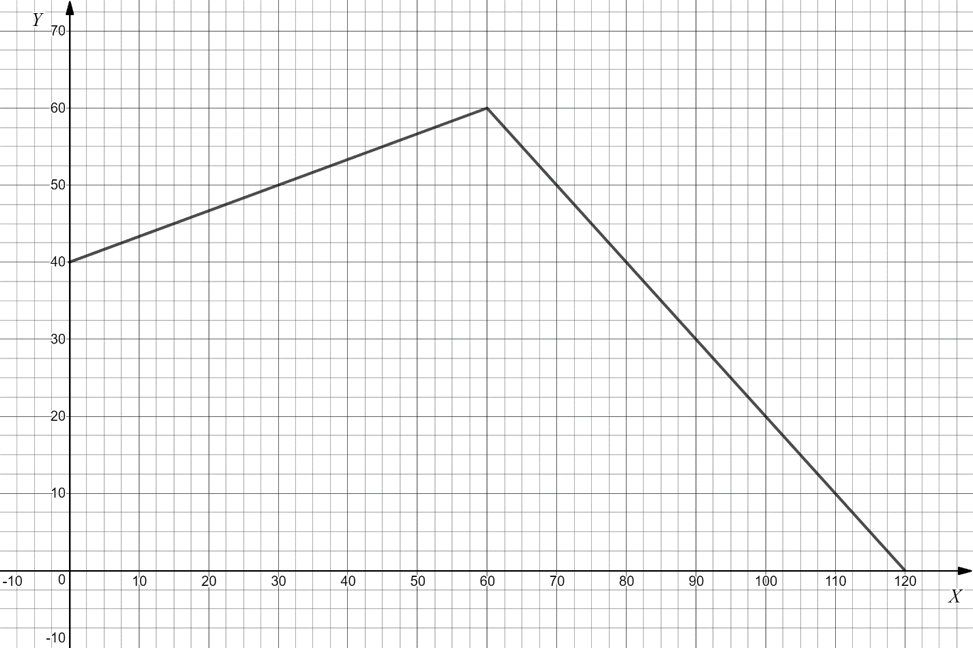
Ниже представлены (для наглядности) графики всех трёх КПВ на одной системе координат.
Красный – предприятие №1
Синий – предприятие №2
Зелёный - ПО

Ответ на третий вопрос
Для начала заметим, что ПО никогда не выберет объём производства X меньше 60, т.к. тогда оно окажется на возрастающем участке КПВ (т.е. сможет увеличить производство обоих товаров сразу).
Также, убывающий участок КПВ представляет собой прямую с коэффициентом -1 при x (т.е. увеличивая производства X на 1, мы отказываемся от одного Y). Т.к. $P_Y=30$, а $P_X=10$, производство каждой дополнительной единицы X (на убывающем участке) будет приносить нам 20ед. убытков. Следовательно, оптимальный объём производства – точка перегиба (60; 60), а $TR_{max}=2400$.
Ответ на четвёртый вопрос
Т.к. убывающий участок КПВ – это прямая с коэффициентом -1 при X.
Для того, чтобы ПО изменило объём производства цена X должна быть больше цены Y.
А для этого она должна увеличиться более чем на 20ед. или более чем в 3 раза.
Ответ на пятый вопрос
Для начало определим максимальное количество ресурса β, которым может обеспечить себя предприятие.
Вспомним, что для ПО: $\beta^+=\frac{2}{3}X$, a максимальное кол-во X = 120.
Следовательно, максимальное кол-во $\beta =\frac{2}{3}*120+80=160$.
(80 – это поставки от города)
Цена Y = 30.
Для того, чтобы предприятие выбрало ненулевой объём производства Y должно выполняться следующее неравенство:
$160*P_{\beta}+120*10<2400$
$160*P_{\beta}<1200$
$P_{\beta}<7,5$
Пояснение: в левой части неравенства – выручка от продажи β и X, а в правой части неравенства – максимально возможная выручка предприятия при данных ценах (а именно – выручка от продажи 60Y и 60X).
Есть другой вариант решения. Заметим, что при уменьшении кол-ва X на 1, мы будем приобретать 20ед. выручки за каждую единицу (из-за того, что Y дороже X на 20 и тангенс угла наклона убывающего участка КПВ = -1).
Также, мы будем терять $\frac{2}{3}\beta$ за каждую единицу X и терять $2\beta$ за производство каждой дополнительной единицы Y. Итого: $\frac{8}{3}\beta$ мы будем терять при движении влево по КПВ.
Отсюда неравенство: $20 > \frac{8}{3}P_{\beta}$
т.е. $7,5 > P_{\beta}$
3. Рынок дроидов на планете Татуин
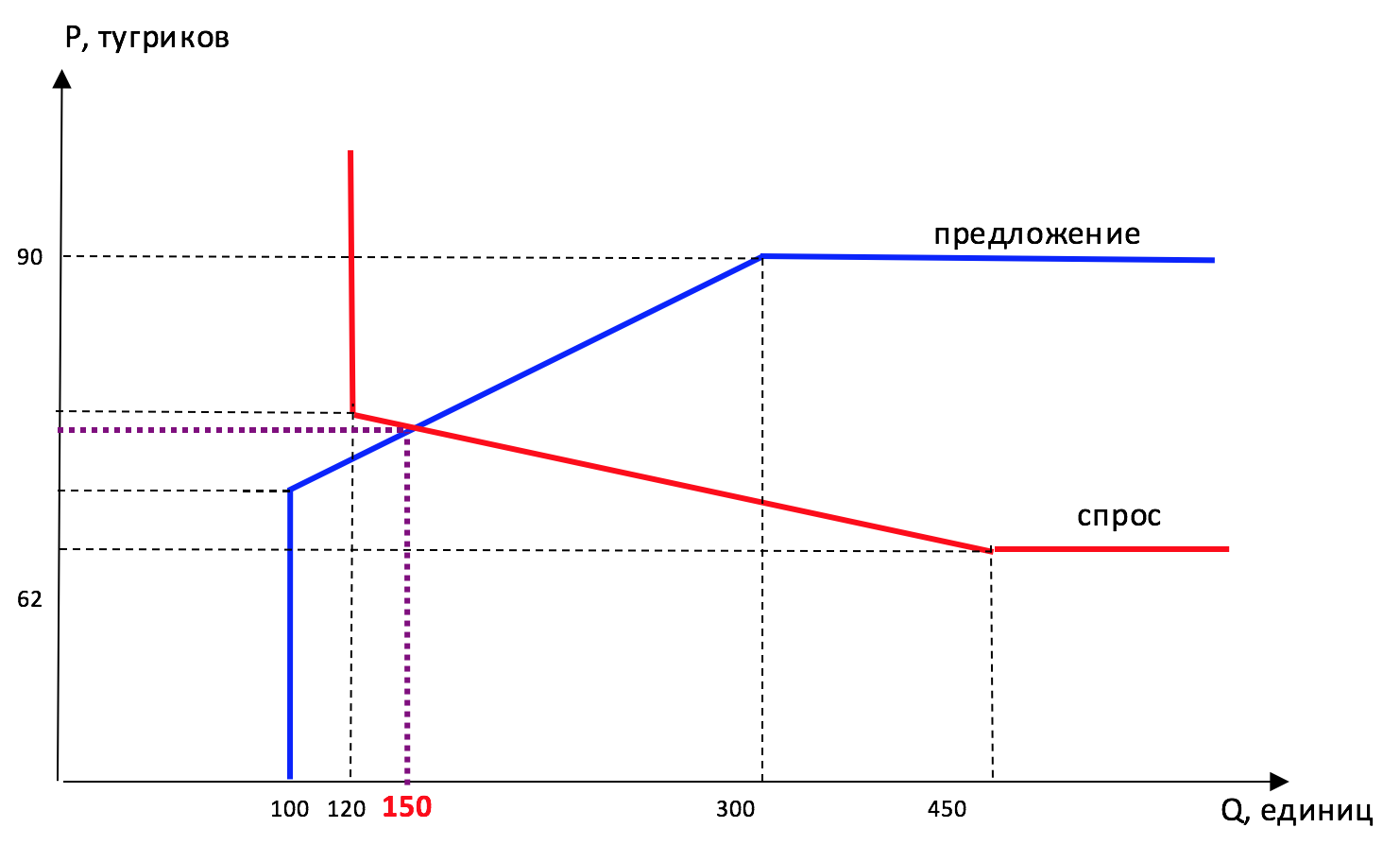
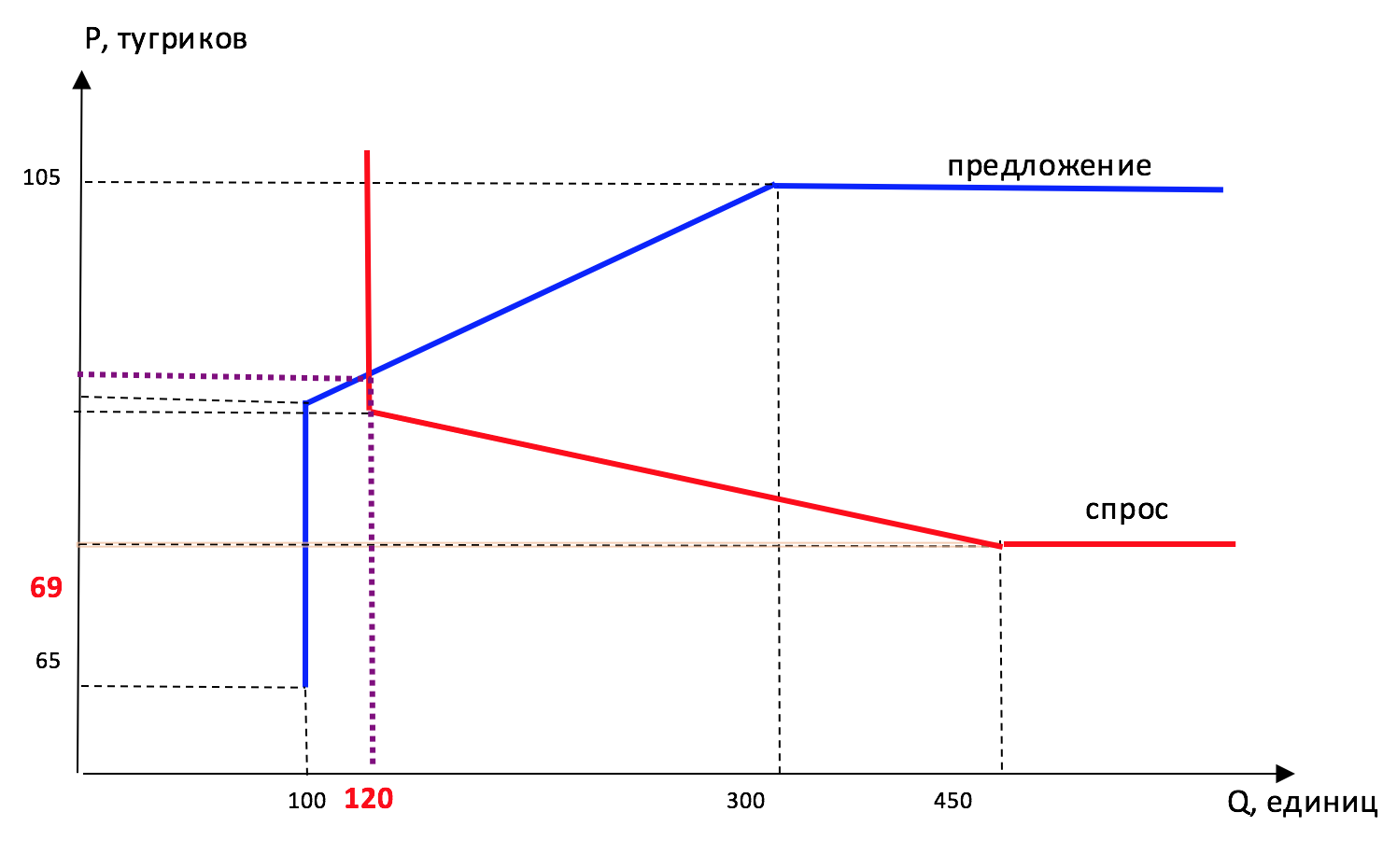
На графике ниже представлена кривая рыночного спроса.
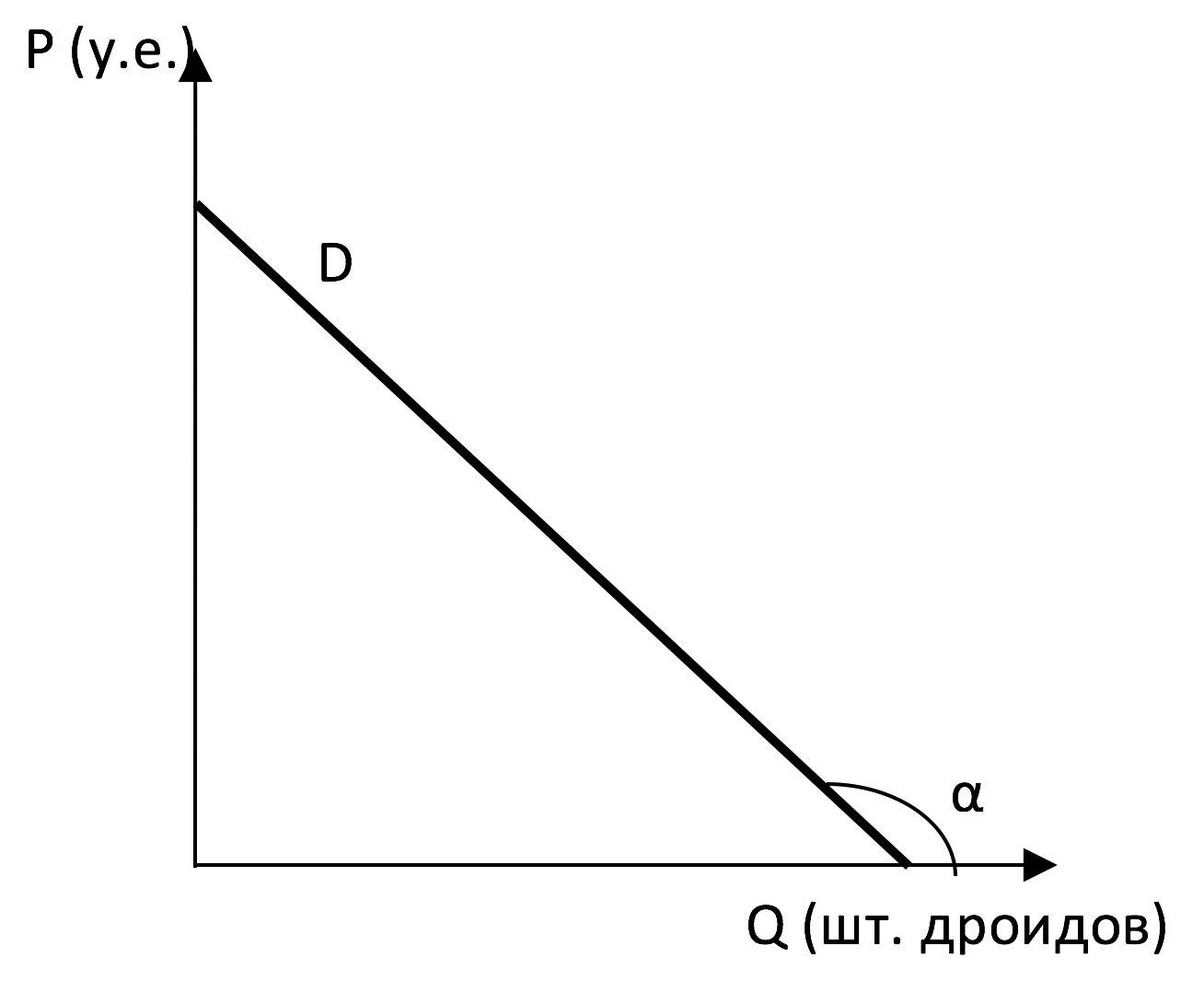
1. Восстановите функции рыночного спроса и рыночного предложения дроидов на планете Татуин.
2. Правительство планеты Татуин должно выплатить Империи 7000 у.е. на строительство звезды смерти (избежать этого никак не получится!). Для сбора данной суммы правительство вводит потоварный налог на производителей дроидов в размере $t$ у.е. с одного дроида. Какую максимальную ставку потоварного налога $t$ может установить правительство, чтобы собрать нужную сумму? Как и на сколько изменится равновесная цена для потребителя?
3. После того, как звезда смерти была достроена, Дарт Вейдер решил использовать ее мощь в своих корыстных целях и стать единственным производителем дроидов на планете Татуин, используя абсолютно новую имперскую технологию. Проведя необходимые расчеты вместе с Императором, они выяснили, что кривая MC представляется линейной функцией. Также было выявлено, что при производстве 100 дроидов предельные издержки равны 300 у.е., а при производстве, максимизирующем прибыль (максимум прибыли достигается только в одной точке), MC=450 у.е. Постоянных издержек производства нет. Какую прибыль получит Дарт Вейдер, монополизируя рынок дроидов на планете Татуин? Покажите решение данного пункта задачи на графике.
По основному тригонометрическому тождеству $\sin^2\alpha+\cos^2\alpha=1 \to \cos^2 \alpha=\pm 0,8$, но так как угол $\alpha$ больше 90 градусов, что соответствует 2 четверти тригонометрического круга, $\cos\alpha=-0,8$.
По формуле приведения $\cos(180-\alpha)=-\cos\alpha \to \cos(180-\alpha)=0,8$
Следовательно,
$tg(180-\alpha)$$=\frac{\sin(180-\alpha)}{\cos(180-\alpha)}$$=\frac{0,6}{0,8}$$=\frac{3}{4}$$=0,75$.
Отсюда $tg \beta =\frac{4}{3}$, следовательно,$Q_d=a-bp=a-\frac{4}{3}p$ ($\beta$ - угол между кривой спроса и осью P).
Эластичность спроса по цене в точке равновесия:
$E^p_d=\frac{dQ}{dP}\times \frac{P_e}{Q_e}=-\frac{4}{3}\times \frac{P_e}{300}=-2 \to P_e=450$
Отсюда $Q_d=a-\frac{4}{3}p=a-\frac{4}{3}\times 450 =300 \to a=900 \to Q_d=900-\frac{4}{3}p$
Координаты точки рыночного равновесия $(Q_e;P_e)=(300;450)$
$E^p_s=\frac{dQ_s}{dp}\times \frac{P_e}{Q_e} \to 3=\frac{dQ_s}{dp}\times \frac{450}{300} \to \frac{dQ_s}{dp}=2 \to Q_s=c+dp=c+2p$
Отсюда: $300=c+2*450=c+900 \to c=-600 \to Q_s=2p-600$
2) Нам известно, что $Q_s=2p-60$, следовательно, после введения потоварного налога $Q_s^1=2(p-t)-600$
$T=7000 \to t*Q_e^1 = 7000 \to t=\frac{7000}{Q_e^1}$
Отсюда $Q_s^1=2(p-\frac{7000}{Q_e^1}-600= 2p - \frac{14000}{Q_e^1}-600$
Так как $tg \beta =\frac{4}{3} \to \frac{Q_e^1}{675-P_e^1} \to 3Q_e^1=2700-4P_e^1 \to P_e^1=\frac{2700-3Q_e^1}{4}$
Отсюда: $Q=2\times(\frac{2700-3Q}{4})-\frac{14000}{Q}-600=\frac{2700Q-3Q^2-28000-1200Q}{2Q}$
Получается $5Q^2-1500Q+28000=0$
$D=1690000 \to \sqrt{D}=1300$
Отсюда $Q_1=20, Q_2=280$
Отсюда получаем $t_1=350, t_2=25$
Следовательно $t_{max}=350$
Отсюда $p_1=660$, следовательно $\Delta p=210$
3) $Q_d=900-\frac{4}{3}p \to p= 675 -0,75 Q \to TR=675Q-0,75Q^2 \to MR=675 - 1,5Q$
Условие максимизации прибыли на рынке монополии $MC=MR$, и если в точке оптимума $MC=450$, то в этой же точке $MR=450 \to 450=675 - 1,5Q \to Q_e=150 \to P_e=562,5$
Восстановим вид кривой $MC$ по двум точкам:
$300=b+100k$ и $450=b+150k$, отсюда $MC=3Q$.
Восстановим уравнение TC:
$TC=\int MC dQ =\frac{3}{2}Q^2 + C$, $C=0$, так как нет постоянных издержек.
Подсчитаем прибыль Дарта Вейдера:
$\pi=TR-TC=150*562,5-\frac{3}{2}150^2=84375-33750=50625 $
Изобразим на графике:
Известно, что $\pi =TR-TC=p*Q-ATC*Q = (p-ATC)*Q$
$ATC=\frac{TC}{Q}=\frac{\frac{3}{2}Q^2}{Q}=\frac{3}{2}Q$
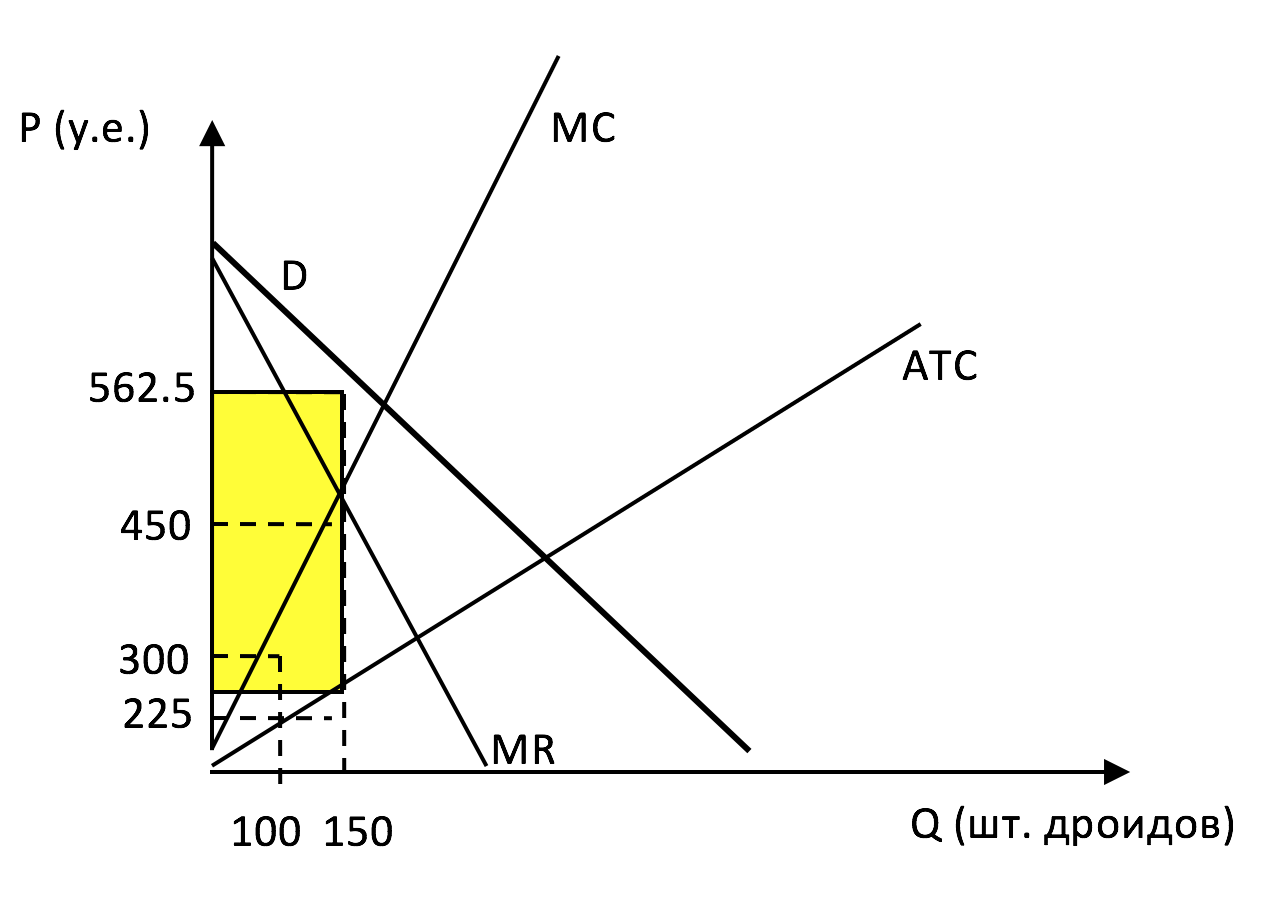
Прибыль – это прямоугольник с вершинами в следующих координатах: (P;Q): (225;0), (562.5;0), (562.5; 150), (225;150); или фигура, выделенная желтым цветом.
4. Неравенство в Некотором царстве
Если бы средний доход бедных увеличился на 50%, а средний доход богатых не изменился, то средний доход во всем царстве возрос бы на 40 монет, а коэффициент Джини сократился до 0,3 (при этом бедные по-прежнему остались бы бедными, а богатые – богатыми).
1. Во сколько раз в Некотором царстве средний доход богатых превышает средний доход бедных?
2. Во сколько раз в Некотором царстве средний доход богатых превышает средний доход всего общества?
- совокупный доход всех бедных равен$ Х_1\cdot \alpha\cdot N$, где N – число жителей Некоторого царства;
- средний доход в царстве равен $ \alpha \cdot Х_1 + (1 – \alpha) \cdot Х_2$;
- совокупный доход всех жителей царства равен $(\alpha \cdot Х_1 + (1 – \alpha) \cdot Х_2) \cdot N$.
Следовательно,
$$ \beta = \frac{\alpha\cdot X-1\cdot N}{(\alpha \cdot Х_1 + (1 – \alpha) \cdot Х_2) \cdot N$} = \frac{\alpha\cdot X_1}{\alpha \cdot Х_1 + (1 – \alpha) \cdot Х_2} $$
Из условия:
$$ K= \alpha - \beta = \alpha - \frac{\alpha\cdot X_1}{\alpha \cdot Х_1 + (1 – \alpha) \cdot Х_2} =0.4 $$
Если бы средний доход бедных возрос на 50%, то доля совокупного дохода царства, которую стали бы получать бедные жители
$$ \beta_1= \frac{\alpha\cdot 1.5 \cdot X_1}{\alpha \cdot 1.5 \cdot Х_1 + (1 – \alpha) \cdot Х_2}$$
Из условия:
$$ K_1 = \alpha - \beta_1=\alpha - \frac{\alpha\cdot 1.5 \cdot X_1}{\alpha \cdot 1.5 \cdot Х_1 + (1 – \alpha) \cdot Х_2} = 0.3 $$
При этом средний доход в царстве стал бы равен $\alpha\cdot 1.5 \cdot X_1+(1-\alpha)\cdot X_2$. А по условию разница средних доходов составляет 40 монет:
$$ \alpha\cdot 1.5 \cdot X_1+(1-\alpha)\cdot X_2 - (\alpha \cdot X_1+(1-\alpha)\cdot X_2) = 0.5 \cdot \alpha \cdot X_1 = 40 \to \alpha \cdot X_1 =80 \text{ } (1)$$
Запишем выражения $K$ и $K_1$, выполнив замену с учетом (1), получим систему уравнений:
$$\begin{cases}
\alpha - \frac{\alpha\cdot X_1}{\alpha \cdot Х_1 + (1 – \alpha) \cdot Х_2} =0.4 \\
\alpha - \frac{\alpha\cdot 1.5 \cdot X_1}{\alpha \cdot 1.5 \cdot Х_1 + (1 – \alpha) \cdot Х_2} = 0.3
\end{cases}$$
Выполним еще одну замену $80 + (1-\alpha)\cdot X_2 =Z $, тогда наша система выглядит намного проще:
$$\begin{cases}
\alpha - \frac{80}{Z} =0.4 \\
\alpha - \frac{120}{Z+40}= 0.3
\end{cases} \to \frac{80}{Z} +0.4 = \frac{120}{Z+40} +0.3 \to \frac{1}{10} = \frac{120Z-80(Z+40)}{Z(Z+40)} \to $$
$$ Z(Z+40) = 120Z-800(Z+40) $$
$$ Z^2 -360Z+32000=0 \to Z_1=200, Z_2=160$$
Если $Z=200$, то $\alpha =\frac{80}{200}+0.4=0.8$, если же $Z_1=160$, то $\alpha = \frac{80}{160}+0.4=0.9$, что не соответствует условию.
Если $\alpha = 0.8$, то из (1) $X_1=\frac{80}{0.8}=100$.
Теперь найдем $Х_2$ (из последней замены):
$$80+(1-0.8)\cdot X_2=200 \to X_2=600$$
А средний доход общества составляет $0.8\cdot 100+0.2 \cdot 600=200$.
Таким образом, средний доход богатых превышает средний доход бедных в 6 раз, а средний доход общества – в 3 раза.