1. Лоббирование
Однако пропорцию обмена можно изменить с помощью лоббирования. Наняв лоббистов, страна А сможет добиться удвоения мировой цены любого из товаров (выраженной в единицах другого товара). Стоимость услуг лоббистов равна 50 единицам Игрека независимо от товара, цену которого страна решит лоббировать.
Назовем кривой торгово-лоббистских возможностей (КТЛВ) множество точек, которое ограничивает сверху множество всех наборов $(x, y)$, доступных стране в результате производства, торговли и лоббирования.
Постройте КТЛВ страны А и выведите аналитическое выражение для данной КТЛВ.
Стране не может быть выгодно лоббировать повышение цены Икса, так как в этом случае она добьется пропорции обмена, равной альтернативным издержками производства внутри страны. А значит, выгод от торговли не будет, а товар Игрек на лоббирование будет потрачен.
Если страна решит лоббировать повышение цены Игрека, то она, конечно, продолжит его экспортировать (экспорт станет еще выгоднее, чем раньше), но потратит на эту операцию 50 единиц Игрека. Получается, что для торговли останется только 150 единиц Игрека, но зато за единицу Игрека можно будет получить 2 единицы Икса. Получаем уравнение КТВ после лоббирования: $X/2+Y=150$.
Такого объяснения получения данного уравнения достаточно, однако возможен и более формальный подход. Предположим, страна будет экспортировать $z$ единиц Игрека. Тогда она получит взамен $2z$ единиц Икса. Получается, что для потребления доступно $Y=150-z$ и $X=2z$. Выражая $z$ из любого из этих условий и подставляя в другое, получаем $X/2+Y=150$.
В каких случаях страна будет применять лоббирование, а в каких не будет? Ответ зависит от того, какая из линий КТВ (без лоббирования или с ним) лежит выше. В первой КТВ $Y=200-X$, во второй $Y=150-X/2$. Составим неравенство:
\begin{gather*}
200-X\ge 150-X/2,\\
X \le 100.
\end{gather*}
Получаем уравнение КТЛВ: (1.1)
\begin{equation}\label{ktv}
Y=\begin{cases}
200-X, & 0\le X\le 100; \\
150-X/2, & 100 < X\le 300.
\end{cases}\end{equation}
Альтернативный способ — составить неравенство, сравнивающее $X$ (так мы узнаем, какая КТВ лежит правее):
\begin{gather*}
200-Y\ge 300-2Y,\\
Y \ge 100.
\end{gather*}
Получаем уравнение КТЛВ: (1.2)
\begin{equation}\label{ktv2}
X=\begin{cases}
200-Y, & 100 \le Y\le 200; \\
300-2Y, & 0 \le Y < 100.
\end{cases}\end{equation}
Выражение (1.1) эквивалентно выражению (1.2), найденному ранее.
Графически ситуация сводится к следующему:
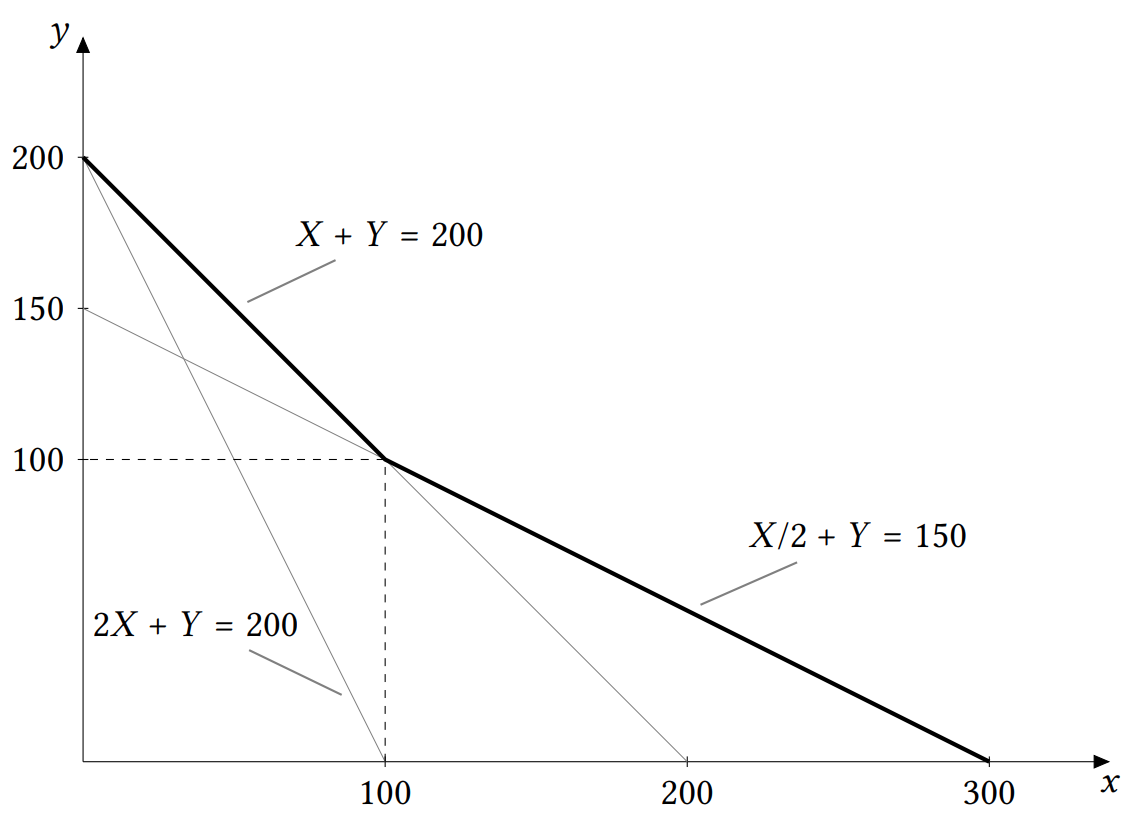
На этом рисунке изображены и подписаны исходная КПВ (не требуется для правильного ответа), КТВ без лоббирования, КТВ с лоббированием. КТЛВ — более толстая линия, состоящая из участков двух КТВ.
Примечание. В обоих вариантах записи уравнения КТЛВ точка $(100, 100)$ может быть отнесена как к верхнему интервалу, так и к нижнему, поскольку КТЛВ является непрерывной функцией. Кроме того, указание нижних и верхних границ ($X\ge 0$, $Y\ge 0$, $X\le 300$, $Y\le 200$) необязательно для корректной записи. Иными словами, следующие варианты, а также аналогичные, также корректны:
\begin{align*}
& Y=\begin{cases}
200-X, & X< 100; \\
150-X/2, & X \ge 100.
\end{cases} &
X=\begin{cases}
200-Y, & Y> 100; \\
300-2Y, & Y \le 100.
\end{cases}
\end{align*}
2. Внезапный центробанк
Заработная плата одного работника фиксирована профсоюзом и составляет \(W\). Совокупный спрос в рассматриваемой экономике описывается уравнением:
\[Y_{AD}=2\frac{M}{P},\]
где $M$ — денежная масса, $P$ — уровень цен.
Центробанк неожиданно применяет меры сдерживающей денежно-кредитной политики, в результате которой новое предложение денег отличается от старого на 36% (профсоюз не успевает скорректировать назначенную им зарплату, количество фирм на рынке не меняется). На сколько процентов и в каком направлении в результате этой меры изменится реальная заработная плата работников?
Прибыль каждой фирмы равна $\pi=Py-WL=Py-Wy^2$. Это парабола с ветвями вниз, максимум которой достигается в вершине: $y=P/(2W)$.
Можно также выразить прибыль не через выпуск, а через количество нанятых работников: $\pi = P\sqrt{L} - WL$. Производная этой функции равна \[\pi ' = \frac{P}{2\sqrt{L}}-W\] и достигает нуля при \[L = \left(P/(2W)\right)^2.\] В этом случае необходимо отметить, что производная убывает (вторая производная отрицательна), а при использовании правила $MRP_L=w$ — что убывает функция $MRP_L(L)$. Поэтому найденное значение $L$ является точкой максимума.
Отсюда получаем фукнцию совокупного предложения всех фирм:
\[ Y_{AS}=\frac{NP}{2W}.\]
Найдем равновесие:
\begin{gather*}
Y_{AD}=Y_{AS}\\
2\frac{M}{P} = \frac{NP}{2W} \\
P=2\sqrt{\frac{MW}{N}}
\end{gather*}
Реальная заработная плата $W/P$ в равновесии равна
\[
\frac{W}{P} = \frac{1}{2} \sqrt{\frac{NW}{M}}.
\]
Если денежная масса меняется со значения $M_0$ до значения $M_1$, а остальные параметры не меняются, то отношение новой и старой реальной заработной платы равно (2.1)
\begin{equation}\label{MM}
\frac{{W}/{P_1}}{{W}/{P_0}} = \frac{ \dfrac{1}{2} \sqrt{\dfrac{NW}{M_1}}}{ \dfrac{1}{2} \sqrt{\dfrac{NW}{M_0}}} = \sqrt{\frac{M_0}{M_1}}.
\end{equation}
Так как описанная в задаче политика сдерживающая, то предложение денег снижается. Следовательно, $M_1=0,64M_0$. Подставляя в формулу (2.1), получаем
\begin{equation}
\frac{{W}/{P_1}}{{W}/{P_0}} = \sqrt{\frac{M_0}{0,64M_0}} = 1,25.
\end{equation}
Получается, что реальная зарплата выросла на 25%.
3. Прибыль — это не всё
Рассмотрим фирму ABC, которая максимизирует не прибыль, а сумму прибыли и величины, зависящей от уровня безработицы в стране:
\[B=\pi+16(100-u),\]
где $\pi$ — прибыль, а $u$ — уровень безработицы в процентах.
Всего в стране проживают 100 человек, 70 из которых стабильно заняты на других производствах и не собираются устраиваться на фирму ABC. 30 человек являются безработными, и фирма ABC наймет сотрудников именно из их числа. (Больше никакие работодатели не предлагают им работу.)
Спрос на продукцию фирмы ABC задается уравнением $Q=120-P$. Фирма производит товар, используя только труд, при этом $Q=2L$. Если фирма наймет $L$ работников, нужно будет платить каждому из них зарплату $w=4L$.
На сколько процентных пунктов в этой ситуации уровень безработицы будет меньше по сравнению с тем, который был бы при максимизации фирмой ABC прибыли?
\[
B=(120-2L)\cdot 2L -4L\cdot L + 16(100-(30-L)).
\]
После упрощения получаем $B=-8 L^2 + 256 L + 1120
$. Это квадратичная парабола с ветвями вниз, вершина которой находится в точке $L^\star=16$.
Тот же ответ можно получить, взяв производную функции ($B '=-16L+256$) и приравняв ее к 0. В этом случае можно заметить, что производная в критической точке меняет знак с + на − (варианты: первая производная убывает, вторая производная равна $-16$, то есть отрицательна), так что это точка максимума.
4. Географическое разнообразие
Издержки перевозки одного пассажира в любой город составляют 2 денежных единицы, не считая издержек организации маршрута. Создание всё новых маршрутов — не такая уж и простая задача, требующая составления расписания, организации логистики, закупок, установки турникетов и т. п. Организация маршрута в первый город стоит 1 денежную единицу, во второй — 2 денежные единицы, ... , в $N$-й город — $N$ денежных единиц.
Определите максимальную прибыль фирмы «Солнышко».
\[ \pi =
(p_1 q_1 - 2q_1) + (p_2 q_2 - 2q_2) + \dots + (p_N q_N - 2q_N) - (1 + 2 +\dots + N).
\]
После подстановки обратных функций спроса $p_i=\frac{20}{\sqrt{q_i}}$ и применения формулы суммы арифметической прогрессии получаем:
\[ \pi =
(20 \sqrt{q_1} - 2q_1) + (20 \sqrt{q_2} - 2q_2) + \dots + (20 \sqrt{q_N} - 2q_N) - \frac{N^2+N}{2}.
\]
Выражение в каждой из скобок — парабола относительно $\sqrt{q_i}$ (каждое $\sqrt{q_i}$ влияет на значение только «своей» параболы). Если $\sqrt{q_i}=t$, то выражения в скобках принимают вид $(20t-2t^2)$. Все параболы имеют вершину в точке $t=5,$ то есть $q_i = 25$.
Тот же ответ можно получить, взяв производную функции прибыли от перевозок до отдельного города:
\[
\pi_i ' = (20 \sqrt{q_i} - 2q_i) '= \frac{10}{\sqrt{q_i}} - 2. \]
Это убывающая функция, а значит, приравнивание ее к $0$ даст максимум выражения под знаком производной: $q_i=25$.
Еще один способ — посчитать прибыль в регионе $i$ как функцию от цены:
\[
\pi_i = p_i \cdot \frac{400}{p_i^2} - 2\cdot \frac{400}{p_i^2}.
\]
Это парабола с ветвями вниз относительно $s=1/p_i$, максимум достигается при $p_i = 4$.
Наконец, можно было узнать оптимальную цену, воспользовавшись формулой взаимосвязи индекса Лернера и эластичности спроса (третий способ):
\[
\frac{p_i-MC}{p_i}= \frac{1}{|\varepsilon|}.
\]
При данных функциях спроса $|\varepsilon|=2$, а $MC=2$ по условию. Отсюда получаем $p_i=4$.
Этот результат никак не зависит от того, каково значение $N$: сколько бы городов ни обслуживала компания, в каждый будет продано 25 билетов, цена каждого билета равна 4.
Запишем функцию прибыли с учетом выбора оптимальных $q_i$:
\begin{equation}\label{pin}
\pi = (20\cdot 5 - 2\cdot 25) \cdot N - \frac{N^2+N}{2} = \frac{99N - N^2}{2}.
\end{equation}
Это тоже парабола с ветвями вниз — теперь уже зависящая от переменной $N$. Ее максимум достигается в вершине — точке $N= 49,5$, но количество городов должно быть целым. Поскольку квадратичная парабола симметрична относительно своей вершины, а числа 49 и 50 находятся на одинаковом расстоянии от 49,5, в двух ближайших целочисленных точках прибыль будет одинаковой и равной
\[ \pi =
\frac{99 \cdot 50 - 50^2}{2} = 1225.
\]