1. Зарплата и производительность
Примеры корректных причин:
- Search: если работник редкой специальности, ему стоит платить больше, чтобы избежать ухода работника к конкуренту и не тратиться на поиск замены; кроме того, нанимать тех, кого надо, проще, если платить им зарплату больше рынка.
- Matching: если работник создает полезные экстерналии, на самом деле или в головах у начальников, ему стоит платить больше (здесь же networking, company image, etc.)
- Winner's curse: если работник создал хорошее впечатление о себе на стадии интервью или получил предложение из конкурирующей фирмы, то зарплата в контракте может быть выше, чем производительность труда, но ниже, чем надо, чтобы начинать сложные процессы переписывания контракта.
- Unions/legislature: если профсоюз, формальный или неформальный, требует <<справедливой>> оплаты, таковая вполне может оказаться не равной производительности труда.
- Expectations/talent hoarding: если фирма ожидает расширения в будущем, имеет смысл нанимать и обучать сотрудников сейчас, даже если с текущим размером фирмы сотрудники не будут слишком заняты.
- Principal-agent: если только суммарный продукт наблюдаем, то непонятно, кого наказывать за отлынивание, и может оказаться выгодней не наказывать.
Ответы, которые не могут работать:
- Экономический цикл: если спрос упал, то производительность труда тоже упадет. а зарплата останется фиксированной. Не работает, потому что в этом случае есть и история про рост спроса, и в среднем производительность труда будет соответствовать зарплате, чего в данных не наблюдается.
- Экономисты, занимающиеся этими исследованиями, не могут принять во внимание сокращенный рабочий день, ненаблюдаемость усилий или продукта, и тому подобного. Это не является экономической причиной.
Каждая корректная причина приносила по одному баллу (но всего не более 5). Экономические термины для указанных явлений было приводить необязательно, достаточно корректного описания.
2. Зарплата больше – работаем меньше
- Молодой писатель стал популярным и издательства значительно увеличили его гонорары за каждую вновь написанную книгу.
- Шахтёр – ударник труда, которому повысили сдельную заработную плату за тонну выработки.
При росте оплаты труда, с одной стороны, увеличивается бюджет, который можно потратить на покупку лишнего часа досуга (что эквивалентно сокращению трудового времени). С другой стороны, стоимость часа досуга возрастает. Если перевешивает эффект увеличения располагаемого дохода, то предложение труда сокращается. Если же перевешивает эффект удорожания часа досуга, то предложение труда растёт.
Рассмотрим теперь предложенные случаи.
Для шахтёра – работника физического труда, который по условию задачи является ударником производства, логично предположить, что он уже работает на пределе физических сил. Соответственно увеличение оплаты труда могло бы простимулировать его работать больше, но он просто физически уже не может увеличить предложение труда.
Для писателя сказать однозначно о превалировании какого-либо из эффектов нельзя, для него увеличение ставки гонорара может привести и к росту продаж книг и к падению.
Дополнительно стоит иметь ввиду, что у писателя существует «нетрудовой» доход, т.е. доход, не зависящий от прикладываемых им усилий к текущему продукту – доход от переиздания ранее проданных книг. Наличие такого дохода, как правило, увеличивает ценность досуга и может склонить чашу весов в пользу снижения занятости.
При проверке учитывались и другие факторы, которые могли оказать влияние на решение об увеличении/уменьшении предложения труда.
Схема оценивания:
- Анализ в разрезе спроса на досуг (3 балла)
- Наличие нетрудового дохода у писателя (1 балл)
- Предельный объем усилий у добытчика (1 балл)
За различные аргументы в пользу того или иного результата начислялось от 0 до 1 баллов в зависимости от уровня аргументации:
- Заработать, пока популярный
- Риск заморозки зарплаты, если перестанет быть ударником труда
- Обоснованный анализ, где именно на кривой предложения находится каждый из агентов
- Эффект показного потребления
- Боязнь снизить качество книг при «валовом» производстве
Не приносят баллы рассуждения:
- Удовольствие от работы
- Различия в уровне цен в местах жительства – так как сравнивается статус-кво с текущей ситуацией для каждого отдельно – безотносительно друг друга.
- Сравнение двух случаев, как если бы они оба выступают на одном и том же рынке труда.
3. Отельные угрозы
В какой-то момент владелец одного из отелей (назовем его Рокф) решил расширить свой отель и увеличить количество номеров в нем вдвое. Согласно его расчётам, при снижении цены на $40\%$ количество туристов в лощину увеличится как раз настолько, чтобы заполнить новые номера.
Понятно, что такие планы не могли понравиться его конкуренту (которого звали Ротш). Ротш несколько раз предлагал соседу не снижать цены, но тот твердо решил расширяться. Тогда Ротш пригрозил также увеличить вместимость своего отеля вдвое и снизить цены, что привело бы выравниванию потока туристов между отелями. Рокф не поверил такой угрозе и начал вести строительство нового корпуса.
Тогда Ротш начал строительство котлована, но Рокф продолжал возводить пристройку. И только когда Ротш начал строить уже второй этаж своего нового корпуса, Рокф пошёл на мировую и согласился сохранять статус-кво. Ротш также решил не расширять свой отель.
- [3 балла] Как вы считаете, почему Рокф не поверил в угрозу Ротша также расширить свой отель?
- [4 балла] Как вы считаете, почему Рокф прекратил стройку, когда Ротш уже строил второй этаж, а не на стадии, когда тот только вырыл котлован?
- [3 балла] Почему Ротш решил не достраивать свой отель, когда Рокф отказался от расширения своего отеля?
Если расширится только один отель, то его владелец получит выгоду в размере $2N\cdot 0{,}6P - C = 1{,}2P\cdot N - C$ у.е. (за счёт роста выручки от новых посетителей, но за вычетом затрат на строительство С), а у конкурента при этом выручка упадет за счет падения цены при неизменной вместимости отеля до $0{,}6P\cdot N$ у.е.
Если же обе гостиницы расширятся, вместимость вырастет, но за счёт дальнейшего падения цены и затрат на расширение выгода обоих в таком сценарии будет ниже, чем в предыдущем случае, выразим её как ($k\cdot P\cdot N-C$) у.е. Вообще, по условию точно рассчитать коэффициент $k$ нельзя, можно только сказать, что он меньше $0{,}6$ (иначе не будет иметь решения пункт b)). Но его размер не принципиален, главное, чтобы выгода от того, что расширятся оба, у Ротша была меньше, чем в случае, когда он не расширяется вообще и просто смотрит на расширение Рокфа, т.е. $P\cdot N \lt k\cdot P\cdot N-C \lt 0{,}6 P\cdot N$.
a. [3 балла] Рокф не поверил Ротшу, поскольку в том случае, когда оба расширяются, выгода Ротша будет меньше, чем если бы он ничего не строил и просто оставил бы Рокфа в покое $k\cdot P\cdot N-C \lt 0{,}6 P\cdot N$.
b. [4 балла] Тут важно, что в каждый момент времени участники оценивают свою выгоду от продолжения строительства. Уже потраченные средства в расчет приниматься не должны, они становятся «невозвратными», или «sunk», издержками. Выгода Ротша от продолжения работ, когда он только вырыл котлован, равна $k\cdot P\cdot N-C_1$, где $C_1$ – издержки, необходимые на завершение проекта. Судя по условию, на стадии котлована понесенные издержки малы, а оставшиеся – велики. Тогда $k\cdot P\cdot N-C_1$ все ещё меньше, чем $0{,}6P\cdot N$, и Ротш может просто оставить всё в таком недостроенном состоянии, и это будет экономически оправданно. Однако в тот момент, когда оставшиеся издержки будут равны разнице между $0{,}6P\cdot N$ и $k\cdot P\cdot N$, Ротшу становится безразлично, бросать строительство или достроить отель до конца и обрушить прибыль обоих магнатов. Как только он потратит на рубль больше, ему становится выгоднее завершить проект, чем бросить его. Рокф в этот момент понимает, что пора договариваться, ведь иначе Рокф не остановится по своей инициативе, он прошёл «точку невозврата».
c. [3 балла] Соглашение об остановке строительства выгоднее соблюдать, ведь если они договорятся, что получат по $P\cdot N,$ а если не договорятся, то обоим достроить выгоднее, чем быть отстающим (по п. b)), и в результате они получат не $P\cdot N,$ а меньше - по $k\cdot P\cdot N-C_1$.
Схема оценивания:
Пункт a
- «не поверил в серьезность» без дальнейших пояснений: 0 баллов
- «т.к. Ротшу это было невыгодно» без дальнейших пояснений или проводится сравнение выгоды Ротша с исходным состоянием, а не состоянием «ничего не делать и смотреть на расширение Рокфа»: $0{,}5$ балла
Примечание: очень многие ошибочно предполагали, что Ротшу не придется снижать цены и думали, что в случае расширения конкурента Ротш всё равно получит выручку $P\cdot N$, и сравнивали её с $0{,}9P\cdot N$. Если при этом чётко не прописывалось словами, что сравнение идёт с состоянием «не строить и смотреть», а упоминалась какая-то первоначальная прибыль или вообще ничего не упоминалось, то выставлялось 0,5 баллов.
- Указано, что выгода Ротша от расширения меньше, чем если бы он ничего не делал, при этом в расчетах допущены различные неточности и ошибки: 1 - 2 балла
Примечание: если считалось, что выручка Ротша не пострадает от действий Рокфа, но сравнивались правильные ситуации, выставлялся балл 1,5.
- Полностью приведено решение: 3 балла
Пункт b
- «до конца не верил в серьезность, а потом поверил» без дальнейших пояснений: 0 баллов
- «Из котлована можно построить что-то ещё» без дальнейших пояснений: 0,5 балла
- «Построить котлован в качестве угрозы менее невыгодно, чем ничего не делать» - 1 балл
- Есть пояснение, почему с определенного момента времени Ротшу выгоднее продолжать строительство, чем не продолжать, упомянуты невозвратные издержки: 3 балла
- Полностью приведено рассуждение из решения: 4 балла
Пункт c
- «Если он решит достроить, то и Рокф достроит» без дальнейших пояснений: 0,5 балла
- «Если он решит достроить, то и Рокф достроит , а это приведет к падению прибыли обоих» без пояснений, почему Рокф тоже достроит: 1 балл.
- Полностью приведено решение: 3 балла
4. Кофейни в Капучиновске
Из-за специфики системы улиц и заграждений в Капучиновске переход между соседними районами возможен только через середину границы между ними, то есть каждый житель города перемещается по нему как ладья по шахматной доске, измеряя при этом расстояния количеством переходов через границу района. Например, жителям района $A4$ нет разницы, в какую кофейню ходить - кратчайший путь до каждой занимает три перехода (пути показаны на рисунке).
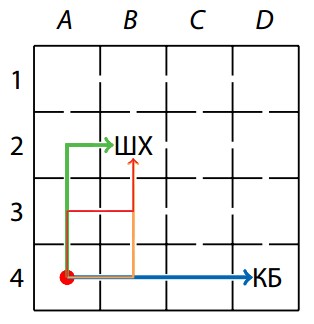
Каждая кофейня получает прибыль в размере 1 доллар с каждой проданной чашки кофе.
а) [3 балла] Найдите значения прибыли, которую получают кофейни «Шоко-хауз» и «Кофебакс».
б) [5 баллов] Город Дабл-Капучиновск отличается от Капучиновска только тем, что он имеет форму квадрата $6\times 6$ (в нём 36 районов: $A1, ..., F6$). Кофейня «Шоко-хауз» расположена в квартале $C2$, «Кофебакс» в квартале $E5$. Фирма «Старладница» собирается построить кофейню в этом городе, при том что законодательство запрещает располагать кофейню в соседнем (по вертикали или горизонтали) районе с уже существующей. Где «Старладница» должна построить кофейню для получения максимальной прибыли, если она ожидает, что после этого будет конкурировать только с «Шоко-хаузом» и «Кофебаксом»?
в) [5 баллов] После того как «Старладница» построила свою кофейню в районе, определенном в пункте $\textbf{б)}$, на рынок решила зайти фирма «Суперчашка», которая также намерена построить кофейню в одном из районов города. Где ей следует это сделать, чтобы получить максимальную прибыль?
г) [7 баллов] Предположим, владелец «Старладницы» предвидел появление на рынке «Суперчашки» и выбирал место для своей кофейни с учетом наличия трёх конкурентов: «Шоко-хауза», «Кофебакса» и «Суперчашки». Как это повлияет на ответы пунктов $\textbf{б)}$ и $\textbf{в)}$?

Чтобы найти прибыль каждой кофейни, достаточно для каждого квартала города определить, где будут пить кофе его жители. Это можно сделать разными способами. Например, можно отметить на рисунке одним цветом все кварталы, жители которых ходят в одну кофейню. Делать это можно в следующей последовательности: сначала для каждой кофейни отметить её цветом все кварталы на расстоянии 1 от неё, затем на расстоянии 2 и т.д. Если в процессе такой разметки окажется, что какой-либо квартал находится на одинаковом расстоянии от обеих кофеен, следует отметить его третьим цветом. После того, как каждый квартал будет окрашен, останется только посчитать прибыли кофеен: 120 за каждый квартал, окрашенный в цвет этой кофейни, плюс $120/2=60$ за каждый квартал третьего цвета. В качестве проверки правильности ответа можно сложить прибыли обеих кофеен и проверить, равняется ли сумма $4\cdot 4\cdot 120=1920$ - общему числу жителей в городе.
Ответ: прибыль «Шоко-хауза» равна 1260, «Кофе-бакса» – 660.
Пункт б
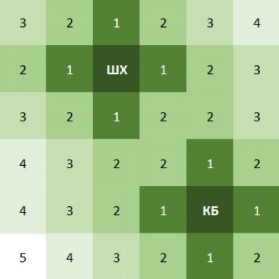
Как и в предыдущем пункте, ответ можно получить разными способами. К примеру, можно снова отметить на схеме города расстояние от каждого квартала до ближайшей уже построенной кофейни, отдельно отметив кварталы, где строительство невозможно. Глядя на такую карту, можно попытаться угадать, где следует построить новую кофейню: логично предположить, что ее выгоднее строить в той части города, жителям которой приходится дальше всех ходить за кофе. Строить кофейню следует так, чтобы в нее ходило как можно больше людей: не только из тех кварталов, до которых в «Старладницу» ходить ближе всего, но и из тех, откуда после ее открытия будет одинаково близко ходить в несколько кофеен. В данном случае наиболее оптимальным кварталом для открытия кофейни является C4 – это можно проверить, сравнив прибыли «Старладницы» в случае открытия в C4 и в любом близлежащем квартале. Расчёты приведены в таблице:
| A | B | C | D | E | F | |
| 1 | 720 | 600 | 600 | 780 | 720 | 600 |
| 2 | 720 | 600 | 660 | 660 | 720 | 600 |
| 3 | 1080 | 1200 | 1260 | 1200 | 1020 | 780 |
| 4 | 1080 | 1200 | 1440 | 1320 | 960 | 780 |
| 5 | 960 | 960 | 1260 | 1200 | 960 | 480 |
| 6 | 840 | 840 | 1020 | 900 | 600 | 600 |
Ответ: «Старладница» должна открыть кофейню в квартале C4.
Пункт в
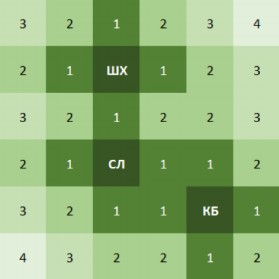
Аналогично предыдущему пункту, можно нарисовать такую же карту с учетом трёх построенных кофеен, а затем таким же образом определить наиболее прибыльное местоположение. Расчёты также приведены в таблице:
| A | B | C | D | E | F | |
| 1 | 480 | 440 | 600 | 760 | 720 | 600 |
| 2 | 480 | 440 | 660 | 640 | 720 | 600 |
| 3 | 840 | 840 | 480 | 900 | 960 | 760 |
| 4 | 820 | 840 | 700 | 480 | 700 | 720 |
| 5 | 720 | 680 | 720 | 580 | 540 | 480 |
| 6 | 580 | 540 | 660 | 660 | 420 | 420 |
Ответ: «Суперчашке» следует открыть кофейню в квартале E3.
Пункт г
Никак не повлияет. В условиях предыдущего пункта каждая из двух вошедших на рынок кофеен обслуживает свои кварталы: «Старладница» – юго-запад города, а «Суперчашка» – северо-восток. При этом нет ни одного квартала, жители которого ходили бы в обе эти кофейни. Иными словами, «Старладница» и «Суперчашка» напрямую не конкурируют друг с другом. В такой ситуации перемещение «Старладницы» приведет лишь к снижению ее прибыли, поэтому она останется в квартале C4. Тогда «Суперчашка» выберет то же самое местоположение, что и в пункте В): E3.
Ответ: Никак не повлияет. «Старладница» как и в пункте б) откроет кофейню в квартале C4, а «Суперчашка» - в E3.
Схема оценивания:
Во всех пунктах баллы за обоснование могут быть снижены в зависимости от степени раскрытия аргументов.
a) 2 балла за верно найденную прибыль любой одной кофейни. 1 балл за верно найденную прибыль оставшейся кофейни. Всего 3 балла.
б) 3 балла за полное и логически верное обоснование расположения Старладницы. 2 балла за верный ответ. Всего 5 баллов.
в) 3 балла за полное и логически верное обоснование расположения Суперчашки. 2 балла за верный ответ. Всего 5 баллов.
г) 4 балла за полное и логически правильное обоснование ответа. 3 балла за верный ответ. Всего 7 баллов. За ответ, в котором было явно указано расположение только одной кофейни, выставлялось 2 из 3 баллов. За ответ «расположение кофеен не изменится» при неверных ответах на пункты б) и/или в) выставлялось 1 или 2 балла из 3.
5. Больничный лист
На фирму господина М хотят устроиться два работника - Данила-мастер и Иван-дурак. Приложив усилия на уровне $x$, Данила-мастер обеспечит господину М выручку (доход) $Y=100+8\sqrt{x}$, а Иван-дурак - выручку $Y=50+4\sqrt{x}$. Господин М не получает дохода и не несёт издержек, если никого не нанимает.
Удовольствие работника можно измерить как разницу между его доходами и уровнем усилий в текущем периоде (если он работает у господина М, то эта разница равна $w-x$). Данила-мастер согласен работать у господина М, если в каждом периоде его доходы превышают уровень приложенных усилий не меньше чем на 64, а Иван-дурак - если в каждом периоде его доходы превышают уровень приложенных усилий не меньше чем на 29.
Господин M легко может отличить Данилу-мастера от Ивана-дурака (он знает, кому предлагает контракт), информация о производительности работников и выручке является общедоступной.
а). [5 баллов] Предположим, что фирма господина М работает только один период, и господин М хочет получить за этот период наибольшую прибыль (разницу между выручкой и издержками). Кого из кандидатов на вакансию он наймет? Какие значения $x$ и $w$ будут записаны в контракте?
б). [10 баллов] Предположим теперь, что фирма господина М функционирует два периода и старается получить максимальную суммарную прибыль. Господин М может предложить работнику только контракт, содержащий одинаковые условия на оба периода, пересматривать контракт после первого периода нельзя. Известно, что Данила-мастер слаб здоровьем и во втором периоде точно заболеет, из-за чего выручка, которую он приносит работодателю, снизится на $25\%$ при любом уровне усилий. Иван-дурак устойчив к болезням, его производительность одинакова в течение обоих периодов.
Если Данила-мастер будет нанят, во втором периоде он сможет воспользоваться больничным листом, в этом случае никаких усилий прилагать будет не нужно, а фирма господина М ничего не заработает и не будет платить зарплату ($x=Y=w=0$ во втором периоде). При этом государство компенсирует Даниле $60\%$ потерянного в связи с болезнью заработка. Данила-мастер уйдет на больничный в том случае, если эта компенсация будет не меньше удовольствия $w-x$, которое он бы получил на работе.
Кого из кандидатов на вакансию наймет господин М, если он знает о том, что Данила-мастер имеет возможность уйти на больничный во втором периоде? Какие значения $x$ и $w$ будут записаны в контракте?
в). [5 баллов] Как изменится ваш ответ на вопрос пункта $\textbf{б)}$, если на период заболевания государственные выплаты по временной нетрудоспособности работника возрастут до $100\%$ от его заработной платы в предыдущий период? Кто выиграет от такого изменения в государственной политике?
г). [5 баллов] В настоящее время в России работники, находящиеся на больничном, получают компенсацию в размере $60\%,\; 80\%$ или $100\%$ своей обычной зарплаты в зависимости от рабочего стажа (при этом если обычная зарплата выше некоторой границы, то проценты считаются от этой границы, а не от всей зарплаты). Исследования показывают, что доля россиян, которые при болезни пользуются больничным листом, составляет меньше 1/5 - остальные продолжают ходить на работу. Объясните, используя экономическую аргументацию, почему люди предпочитают не брать больничный лист.
Поэтому максимизируя прибыль работодателя при условии $w-x = u_0$
$$ \begin{array}{c} \pi^{D}_1=\pi^{D}_2 = 100+8 \sqrt{x} - 64 -x \to \max \\
\pi^{\text{И}}_1=\pi^{\text{И}}_2 = 50+4 \sqrt{x} - 29 -x \to \max \end{array}$$
мы найдём контракт для высокопроизводительного работника $(w^{D}, x^{D}) = (80, 16)$ которому соответствует прибыль $\pi^{D}_{1, 2}=52$ и для низкопроизводительного $(w^{\text{И}}, x^{\text{И}}) = (33, 4)$ которому соответствует прибыль $\pi^{\text{И}}_{1, 2}=25$. Господин М предложит контракт $(w^{D}, x^{D}) = (80, 16)$ для высокопроизводительного работника. Будет нанят Данила-мастер.
б). [10 баллов] Поскольку условия контракта пересматривать нельзя, господин $M$ будет максимизировать суммарную прибыль двух периодов. Если Данила-мастер возьмет больничный, то $\pi^{D}_{1}=52$, $\pi^{D}_{2}=0$, но суммарная прибыль, $\pi^{D} =52$ больше, чем прибыль при найме Ивана $ \pi^{\text{И}} = \pi^{\text{И}}_1+\pi^{\text{И}}_2 = 25 \cdot 2=50$. Если же Данила-мастер останется на работе, то снижение производительности работника обеспечит господину М во второй период выручку в размере $0{,}75 \cdot Y^{D}$ и суммарная прибыль господина $M$ составит $ \pi^{D}= \pi^{D}_1+\pi^{D}_2 = Y^{D} + 0,75 \cdot Y^{D} - 2\cdot w^{D}$, максимизируя которую
$$\pi^{D}= 175+ 14 \sqrt{x} -128 -2x \to \max$$
господин М предложит Даниле-мастеру контракт $(w^{D}; x^{D}) = (76{,}25 ; 12{,}25)$.
Данила-мастер, в свою очередь, заболев и оставшись на работе, получит удовольствие, равное резервному $w-x=u_0$. Если же он выйдет на больничный, то получит 60% оплаты труда, и удовольствие, равное $0{,}6\cdot w$. Условие выхода на больничный: $0{,}6\cdot w>w-x$ не выполняется, то есть он предпочтёт работать ($80 \cdot 0{,}6 = 48 \lt 64$ , $76{,}25 \cdot 0{,}6 = 45,75 \lt 64$). Господин $M$, зная это, предложит Даниле мастеру контракт $(w^{D}; x^{D}) = (76{,}25 ; 12{,}25)$ и получит прибыль $\pi^{D}=71{,}5.$
в). [5 баллов] При 100% оплате больничного листа работник предпочтет уйти на больничный, получив от этого удовольствие, большее, чем от альтернативного вида занятости, что снизит прибыль нанимателя до 0 во второй период и до 52 д.ед. за оба периода. Но и в этом случае работодатель в первый период наймет высокопроизводительного работника, предложив ему контракт $(w^{D}, x^{D}) = (80, 16)$. Выиграет Данила-мастер, получивший не только контракт с более высокой зар. платой и уровнем усилий для первого периода (по сравнению с п. б), но и возможность отдыхать не теряя в заработке. Работодателю придется смириться с потерей прибыли. Государство выплатит большую компенсацию.
Работник с меньшей производительностью, но более здоровый мог бы выиграть, если бы был нанят вместо высокопроизводительного работника (если бы в условии были другие числа, например, $Y^{\text{И}} = 60 + 6\sqrt{x}$)
г). [5 баллов] Возможные причины не покидать рабочего места в период болезни:
1. Несоответствие реальных условий условию задачи:
1.1. Фактический уровень оплаты часто зависит от результатов труда работника. А если работник не выходит на роботу, то и результаты соответствующие, то есть несмотря на то, что работник в текущий момент получает «полную компенсацию», он теряет на будущем повышении оплаты или премиях.
1.2. Человек на работе получает не только материальную компенсацию, но и моральное удовлетворение от работы. Не выходя на работу, человек «недополучает» морального удовлетворения.
2. Альтернативные издержки ухода на больничный:
2.1. Получение больничного листа требует дополнительных усилий и морального напряжения. Например очереди в поликлинике, на которые тратится не только время, но и нервы (окружающие больные часто выливают вокруг себя изрядную порцию негатива), а также здоровья (вероятность подхватить дополнительную инфекцию в поликлинике гораздо выше, чем в здоровом обществе).
2.2. В России на многих рабочих местах сохраняется практика получения «серой» зарплаты. В этом случае уход на больничный для работника означает снижение его дохода и может побуждать оставаться на работе даже при значительном ухудшении самочувствия.
2.3. Отсутствие у работодателя возможности заменить заболевшего сотрудника приводит к снижению его дохода и вызывает резонное недовольство часто болеющими сотрудниками. Это повышает для сотрудника риск быть уволенным.
3. Другие причины:
Например, часто возникают ситуации, когда обязанности отсутствующего сотрудника все же необходимо выполнять, и они возлагаются на других работников без соответствующего этому увеличения их заработка, что приводит к напряженной обстановке в коллективе и может значительно снижать его производительность.
Схема оценивания:
Пункт а
- Определено, что нанят Данила (1 балл)
- Верно найдены значения (x, w) при найме Данилы (3 балла)
- Решение четко обосновано (1 балл)
Арифметические ошибки – (-1) балл
Пункт б
- Определено, что нанят будет Данила (1 балл)
- Верно найдены значения (x, w) при найме Данилы если он не берёт больничный (6 баллов)
- Определено условие, при котором Данила возьмет больничный ($w \lt 2{,}5x$) или другим способом обоснованы его предпочтения относительно работы и ухода на больничный (1 балл)
- Произведено сравнение прибылей в случае найма Ивана или Данилы (1 балл)
- Решение чётко обосновано и не содержит других существенных недочётов (1 балл)
Пункт в
- Определено, что при 100% оплате больничного работник предпочитает уйти на больничный (1 балл)
- Верно определены прибыли работодателя при найме каждого из работников (1 балл).
- Определено, кто будет нанят (Данила) и выписаны условия контракта с этим работником $(x, w)=(16, 80)$ и прибыль фирмы за два периода $\pi=52$ (1 балл)
- Дан ответ на вопрос «кто выиграет?» (2 балла)
Пункт г
- Определена и экономически аргументирована 1 причина - (3 балла)
- Определены и экономически аргументированы 2 разноплановые причины - (4 балла)
- Определены и экономически аргументированы как минимум 3 разноплановые причины - (5 баллов)
6. Оптовый рынок электроэнергии
Объём нагрузки электростанции измеряется в мегаваттах (МВт) - мощности энергии, которую вырабатывает станция в каждый конкретный момент времени. Выработка станции измеряется в МВт$\cdot$ч, то есть если, например, станция несла нагрузку 60 МВт в течение 24 часов, то она выработала 1440 МВт$\cdot$ч.
Параметры вашей электростанции таковы:
- $P_{\min} = 60$ МВт - объём нагрузки, ниже которого станция нести не может;
- $P_{\max} = 100$ МВт - установленная мощность станции, объём нагрузки выше которой она нести не может;
- Себестоимость производства в пределах $P_{\min}$ составляет 350 руб. в час за МВт.
- Себестоимость производства дополнительной электроэнергии свыше $P_{\min}$ (но не более $P_{\max}$) составляет 650 руб. в час за МВт.
Например, если станция 1 час работала с нагрузкой 60 МВт и 1 час с нагрузкой 100 МВт, то суммарная выработка за 2 часа составила 160 МВт$\cdot$ч, а издержки производства составили $60\cdot 350+60\cdot 350+40\cdot 650=68~000$ руб.
Нагрузка потребления ($C$) каждые сутки составляет $70\%$ от суммарного значения $P_{\max}$ всех участников рынка.
Каждый участник конкурса должен определить, какую цену за МВт$\cdot$ч своей электроэнергии он укажет в заявке. Системный оператор (регулирующий орган, определяющий, какие станции будут работать в течение суток) собирает все заявки и отбирает столько станций с самой дешевой энергией, чтобы их суммарный $P_{\max}$ был не ниже $110\%$ нагрузки потребления. Таким образом, если отобрано $N$ станций, то выполняются следующие условия:
\[\begin{equation}
N\cdot P_{\max} \ge C\cdot 1{,}1; \\
(N-1)\cdot P_{\max} \lt C\cdot 1{,}1.
\end{equation}\]
Нагрузка каждой станции определяется системным оператором следующим образом. Станции с самыми дорогими заявками несут нагрузку на уровне $P_{\min}$, а станции с самыми дешевыми - на уровне $P_{\max}$. Если при этом количество станций каждого типа можно подобрать таким образом, чтобы их суммарная нагрузка была равна нагрузке потребления, то рыночная цена электроэнергии определяется исходя из самой дешевой заявки станций с нагрузкой $P_{\min}$ (такая станция называется ценозамыкающей). В ином случае одна из станций (последняя из тех, чьи заявки можно отнести к дорогим) загружается на уровне между $P_{\min}$ и $P_{\max}$ и становится ценозамыкающей.
Все включенные станции получат оплату по цене, равной ценовой заявке ценозамыкающей станции. Станции, которые не были отобраны на рынке, остаются выключенными, то есть не получат оплату и не несут издержек.
Ваша задача — указать цену вашей заявки в специальной форме на сайте конкурса. После того как заявки всех участников конкурса будут обработаны, вы получите 1 балл за каждые 50000 руб. прибыли вашей электростанции.
1) Цена в диапазоне [0; 350) руб./МВтч
2) Цена ровно 350 руб./МВтч
3) Цена в диапазоне (350; 650) руб./МВтч
4) Цена ровно 650 руб./МВтч
5) Цена выше 650 руб./МВтч
Сравним диапазоны 1) и 2).
Если результирующая цена на рынке больше 350, то разницы между двумя заявками нет – в любом случае станция будет работать на $P_{\max}$.
Если результирующая цена меньше 350, то работать невыгодно даже на $P_{\min}$, и соответственно надо ставить заявку больше замыкающей заявки, чтобы не отобраться. Т.е. из двух предложенных опций лучше выбрать ровно 350.
Если цена ровно 350, то опять-таки из двух опций следует выбирать вторую, т. к. в в этом случае есть шанс, что мы будем работать не на $P_{\max}$, а окажемся замыкающей станцией, т. е. понесём меньшие убытки на дозагрузке.
Таким образом 2-й диапазон всюду предпочтительнее первого.
Рассмотрим диапазон 3).
Подавая такую ценовую заявку, мы хотим работать ровно на $P_{\min}$. Если результирующая цена ниже или равна 350, мы не отберёмся и нам это выгодно. Если результирующая цена окажется выше нашей заявки, то мы будем работать на $P_{\max}$ и получим неэффективную работу в дозагрузке. И только если цена окажется в диапазоне от 350 до нашей заявки, мы получим загрузку, отвечающую нашему целеполаганию от такой заявки. Таким образом, нам выгодно сдвигать заявку в этом диапазоне как можно выше, до 650, чтобы увеличить интервал, в котором сидит благоприятный для нас исход. Единственная опасность – попасть в категорию самых дорогих (неотобранных).
Ставка 650 – это предел реализации стратегии из 3-го диапазона. Если мы отберёмся – мы гарантированно не получим убытка на дозагрузке.
Ценовая заявка выше 650 – это, с одной стороны, желание заработать и на $P_{\max}$, с другой – риск не отобраться вообще.
Соответственно у участников было три стратегии, которые стоило выбирать в зависимости от их веры в соотношение между рискованными и осторожными игроками.
350 – практически гарантированная работа на $P_{\max}$, но с потерями в дозагрузке (гарантия, что заработаешь больше 0)
Диапазон от 350 до 650 – вероятность загрузки на $P_{\max}$ с убытком зависит от доли осторожных игроков – чем их больше тем больше вероятность загрузиться с убытком, но тем меньше вероятность неотбора.
Ставка больше 650 – риск неотбора; чем больше осторожных игроков, тем выше риск.
Схема оценивания:
В ситуации Конкурса-2017 всего на рынке присутствовали 82 генератора. Из них 9 подали заявку ниже 350, ровно 350 – 1 генератор, от 350 до 650 – 41 генератор, ровно 650 – 2 генератора, остальные выше.
64 генератора были отобраны в рынок, цена самого дорого отобранного составила 780 руб/МВт$\cdot$ч. Таким образом 18 генераторов были не отобраны и получили 0 баллов. Цена замыкания составила 594 руб./МВт$\cdot$ч, т.е. все генераторы, кто подавал заявку ниже этой цены работали на $P_{\max}$ и теряли деньги, работая в дозагрузке (получали 6 баллов) – таких генераторов 47.
Ценозамыкающий генератор загрузился лишь частично и получил 6,5 баллов.
Все подавшие заявку в диапазоне от 594 до 780 (16 генераторов) работали на $P_{\min}$ и получили 7 баллов.