1. Онлайн-вклады
- «Снижение издержек». Отсутствие необходимости физического проведения операций, связанных с открытием онлайн-вклада, снижает издержки, связанные с функциональной деятельностью банка по открытию и обеспечению таких вкладов. Фактически, банки предлагают две разные услуги (обычный вклад и онлайн-вклад), осуществление которых связано с различными предельными издержками. Цены на такие услуги различаются.
- «Ценовая дискриминация». Поскольку условия вкладов, открытых лично или через онлайн-сервис, одинаковы за исключением цены предоставляемой услуги, можно считать, что банк, начисляя разный процент на депозит, осуществляет ценовую дискриминацию. Тем самым он привлекает новых клиентов, которые не готовы нести издержки, связанные с открытием вклада при личном присутствии в отделении банка, и не готовы оформить даже онлайн-вклад по "очному " проценту.
- Последний аргумент является существенным. Открытие онлайн-вкладов значительно снижает издержки для той группы людей, у которых высоки альтернативные издержки, связанные с использованием свободного времени. Для тех людей, которые ценят удобство открытия онлайн-вкладов, нет смысла повышать процент по вкладу, они согласились бы и на меньший, по сравнению с "очным ", процент по депозиту, что, безусловно, было бы выгодно банку. Однако банк повышает процент, а не снижает его, что преследует своей целью привлечь именно новых клиентов, тех, кто не готов класть деньги на депозит дистанционно даже по "очному " проценту. Поскольку повышение процента привлекает всех клиентов банка, которые готовы пользоваться интернет-сервисом, а не только тех, у кого высоки альтернативные издержки использования свободного времени, и поскольку у банка нет возможности идентифицировать клиентов и предлагать им разные проценты по вкладам, разница в процентах по "очному " вкладу и онлайн-вкладу не может быть значительной.
- «Плата за риск». Возможность осуществлять онлайн-вклады появилась в России относительно недавно. Большое количество людей относится с недоверием к подобному вложению средств. Чтобы стимулировать их принять решение в пользу онлайн-вкладов (что, в свою очередь, может снижать операционные издержки банка) банки предлагают им более выгодные условия по депозитам. При отсутствии повышенной ставки такие клиенты отказались бы осуществлять онлайн-вклады. Таким образом, повышая процент по вкладу, банк оплачивает риск недоверчивых клиентов. По указанной в предыдущем пункте причине разница в процентах по "очному " вкладу и онлайн-вкладу не может быть значительной.
2. Три тарифа
| Тариф |
"Обычный" |
"Новогодний" | "Рождественский" |
|---|---|---|---|
| Цена звонков (руб/мин) |
5 | 2 | 8 |
| Цена СМС (сообщ/мин) |
3 | 7 | 1 |
У разных жителей города разные потребности в услугах Еле2: кому-то нужно больше звонить, другие общаются в основном посредством SMS, кто-то активно пользуется обоими видами связи, а некоторые предпочитают личное общение. Пусть $x$ — количество минут звонков, которое в течение месяца совершает житель города, а $y$ — количество текстовых сообщений, которое он отправляет (эти параметры для каждого жителя не зависят от цен на услуги связи). Каждый житель может выбрать только один тариф. Определите для всевозможных пар $(x, y)$, таких что $0\le x\le 1000$ и $0\le y\le 1000$, какой тариф выберет житель города для минимизации своих расходов на связь. Для наглядности отметьте в координатах $(x, y)$ множества точек, соответствующие выбранным тарифам (если бывают такие пары $(x, y)$, для которых оптимальными являются несколько тарифов, отметьте и подпишите эти множества тоже).
$$ f_1(x,y) = 5x+3y ; \quad f_2(x,y) = 2x+7y; \quad f_3(x,y) = 8x+y .$$
Попарно сравним эти издержки:
$$ 1) \quad f_1(x,y) \leq f_2(x,y) \Leftrightarrow 5x+3y \leq 2x+7y \Leftrightarrow 3x-4y \leq 0. $$
$$ 2) \quad f_1(x,y) \leq f_3(x,y) \Leftrightarrow 5x+3y \leq 8x+y \Leftrightarrow 3x-2y \geq 0. $$
$$ 3) \quad f_2(x,y) \leq f_3(x,y) \Leftrightarrow 2x+7y \leq 8x+y \Leftrightarrow x-y \geq 0.$$
Таким образом, тариф "Обычный" не хуже двух других на множестве $$\left\{(x,y) \mid \frac{3x}{4} \leq y \leq \frac{3x}{2}, ~ 0\leq x,y\leq 1000\right\},$$
тариф "Новогодний" не хуже двух других на множестве $$\left\{(x,y) \mid y \leq \frac{3x}{4}, ~ 0\leq x,y\leq 1000\right\},$$ тариф "Рождественский" не хуже двух других на множестве $$\left\{(x,y) \mid y \geq \frac{3x}{2}, ~ 0\leq x,y\leq 1000\right\}.$$
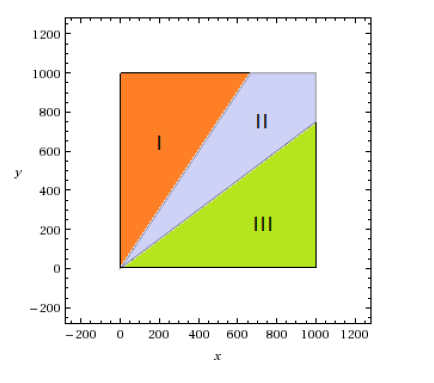
На плоскости $(x,y)$ области оптимальности тарифов выглядят так, как показано на рисунке. В области I оптимальным является тариф "Рождественский", в области II оптимальным является тариф "Обычный", в области III оптимальным является тариф "Новогодний". На границе областей I и II самыми выгодными тарифами являются "Рождественский" и "Обычный", а на границе областей II и III самыми выгодными тарифами являются "Обычный" и "Новогодний".
3. Опрос
- воспользоваться имеющейся у него базой данных со списком адресов и домашних телефонов всех жителей города: случайным образом выбирать людей и звонить им, пока не наберется 500 ответивших человек;
- опросить по телефону отдельно 300 жителей Спального района, 150 жителей Центра и 50 жителей Частного сектора, выбрав их случайным образом из имеющейся у Васи базы данных со списком адресов и домашних телефонов всех жителей города;
- нанять 10 студентов, отправить их в 10 самых населенных домов N-ска и дать задание каждому студенту опросить по 50 жителей своего дома.
Вася должен провести высококачественное исследование — это первый приоритет Васи (халтуру заказчики не примут). С другой стороны, Вася хотел бы сэкономить на проведении опроса (при условии, что он будет высококачественным), потому что его гонорар не зависит от того, сколько денег он потратил в процессе работы.
а) Предположим, Васе нужно узнать средние расходы на пирожные в N-ске в целом. Какой метод вы бы посоветовали ему выбрать?
б) Предположим, Васе нужно узнать средние расходы на пирожные жителей каждого района N-ска по отдельности. Какой метод вы бы посоветовали ему выбрать?
Во втором варианте (опросить 300 жителей Спального района, 150 жителей Центра и 50 жителей Частного сектора) используется смещённая выборка: доля опрошенных по каждому из районов (от числа всех опрошенных) не соответствует доле жителей, проживающих в этом районе (от числа всех жителей в городе). Например, в Частном секторе проживает $2/(100+10+2)\approx 1{,}7$ % от всех жителей города, но среди опрошенных их будет $50/(300+150+50) = 10$ % (от всех опрошенных). Если в разных районах расходы на пирожные существенно различаются (а этого разумно ожидать, поскольку в указанных районах скорее всего живут люди с разным социально-экономическим статусом), это приведёт к тому, что среднее по такой выборке не будет равняться среднему по всему городу. Например, если предположить, что в Центре расходы на пирожные на одного человека в среднем составляют 5 тыс. рублей в месяц, в Спальном районе 2 тыс. рублей в месяц и в Частном секторе 10 тыс. рублей в месяц, то средние расходы по городу составят
\[
5\cdot\frac{10000}{112000}+2\cdot\frac{100000}{112000}+10\cdot\frac{2000}{112000}\approx
2{,}41\text{ тыс. руб./мес.},
\]
а средние расходы по нашей выборке:
\[
5\cdot\frac{300}{500}+2\cdot\frac{150}{500}+10\cdot\frac{50}{500}=4{,}6\text{ тыс. руб./мес.}
\]
Такое расхождение в результатах свидетельствует о некачественности опроса при использовании второго метода. В силу того, что качество является первым приоритетом, мы не можем использовать этот метод.
Наконец, в третьем варианте (отправить студентов в 10 самых населённых домов) выборка также будет смещена: 10 самых населённых домов скорее всего находятся в Спальном районе (именно там находятся многоэтажки) и результат вообще не будет учитывать потребление пирожных в других районах (которое может существенно отличаться от потребления в Спальном районе). Таким образом, этот метод также нельзя рекомендовать.
Если выйти за рамких предложенных методов, то можно предложить модификацию второго: либо скорректировать квоту по каждому району так, чтобы она соответствовала доле жителей этого района во всём городе (то есть опросить 446 человек из Спального района, 45 человек из Центра и 9 человек из Частного сектора), либо использовать исходную выборку, но скорректировать результат, посчитав отдельно средние по каждому из районов, а затем сложив их с весами, равными доле населения соответствующего района во всём городе: то есть результат по Спальному району умножить на $100/112\approx 0{,}89$, результат по Частному сектору умножить на $2/112\approx 0{,}02$ и результат по Центру умножить на $10/112\approx0{,}09$, и всё сложить. Такой подход может дать даже лучший результат (имеющий меньшую дисперсию, то есть менее зависящий от случайности),
чем первый из предложенных методов, при условии, что в разных районах расходы на пирожные различаются сильно.
Ответ: первый метод (или модифицированный второй).
б) Если нас интересует среднее по каждому из районов, то оптимальным является второй подход. Как обсуждалось выше, третий подход скорее всего даст информацию только по одному району и поэтому заведомо не подходит. Первый подход в этом случае не оптимален: он больше подвержен случайности — например, может так случиться, что в результате случайного выбора наберётся совсем мало респондентов из Частно сектора и в этом случае данные по этому району будут очень ненадежны (вдруг нам случайно попадётся один человек и он окажется большим сладкоежкой?).
Ответ: второй метод.
4. «Маскилон»
Какое количество каждого товара следует произвести «Маскилону», чтобы получить максимальную прибыль?
$$
\pi_\text{к}=(100-q_\text{к})q_\text{к}-q_\text{к}^2-2q_\text{к}=-2q_\text{к}^2+98q_\text{к}
$$
Максимальное значение квадратичной функции с отрицательным старшим коэффициентом достигается в точке $q_\text{к}^*=24{,}5$.
На рынке ракет-носителей "Маскилон" максимизирует функцию прибыли
$$
\pi_\text{р}=(40-q_\text{р})q_\text{р}-4q_\text{р}=-q_\text{р}^2+36q_\text{р}
$$
Максимальное значение этой квадратичной функции с отрицательным старшим коэффициентом достигается в точке $q_\text{р}^*=18$.
С учетом ограничения транспортных мощностей "Маскилону" нет смысла производить более 20 космических кораблей или более 10 ракет-носителей. Значит, оптимальный с учетом транспортных ограничений уровень выпуска на каждом из двух рынков будет лежать на участке возрастания прибыли на соответствующем рынке. Отсюда следует, что в оптимуме "Маскилон" полностью задействует свои транспортные мощности.
Пусть "Маскилон" производит $n$ ракет-носителей. Тогда, так как задействуются все транспортные мощности, он произведет $2(10-n)$ космических кораблей. При таком уровне выпуска товаров общая прибыль фирмы будет равна
$$
\pi=-n^2+36n-2(2(10-n))^2+98\cdot 2(10-n)=-9n^2+1160
$$
При неотрицательных $n$ функция прибыли убывает по $n$. Значит, "Маскилон" произведет 0 ракет-носителей и 20 космических кораблей.