Введём функцию спроса: $Q_d=a-b\cdot p$ и функция предложения:$Q_s=c+d\cdot p$ Из условия задачи следует, что $b=d$(2 балла). Тогда равновесная цена равна
$(a ‒ c)/2b$. При вдвое большей цене молоко никто не покупает, отсюда (3 балла), откуда $с = 0$, то есть кривая предложения проходит через начало координат. С другой стороны, при цене $(a ‒ c)/b = a/b$ величина предложения равна 10, откуда $0+b\cdot (a/b)=10$ (3 балла), то есть
$a = 10$. Равновесное количество равно $а ‒ b\cdot (a ‒ c)/2b = a/2 = 5 $(2 балла).

Спрос будет задаваться кусочно-линейной функцией:
$$Q=\begin{cases}
48-4p,p \in [0,8] \\
32-2p,p \in [8,16]
\end{cases}$$ (2 балла).
Тогда обратное уравнение спроса: $P=\begin{cases}
16-Q/2, Q \in [0,16] \\
12-Q/4, Q \in [16,48]
\end{cases}$ (2 балла).
Общие издержки фирмы, согласно условию, задаются уравнением $TC=6Q$
(1 балл).
Тогда прибыль фирмы устроена следующим образом:
$$\pi=\begin{cases}
Q(16-Q/2)-6Q, Q \in [0,16] \\
Q(12-Q/4)-^Q, Q \in [16,48]
\end{cases}$$ (1 балл).
Максимум функции на отрезке [0,16] достигается в вершине: Q=10 и равняется 50 (2 балла).
Максимум функции на отрезке [16,48] достигается на границе отрезка: Q=12, значение не принадлежит выбранному отрезку (2 балла).
Таким образом, фирма будет производить 10 единиц по цене 11, а спрос на продукцию фирмы будет предъявлять только вторая группа потребителей.

Можно решать задачу, используя обратную функцию спроса.
Тогда функция прибыли от цены имеет вид:
$$\pi (p)=\begin{cases}
(48-4p)(p-6),p \in [0,8] \\
(32-2p)(p-6),p \in [8,16]
\end{cases}$$ (5 баллов).
Каждый участок функции прибыли ‒ парабола с ветвями вниз, вершина первой параболы в точке p = 8, вершина второй параболы в точке p = 11 (обе координаты принадлежат соответствующим участкам). Поскольку прибыль
в точке (8, 32) лежит и на второй части тоже, можно заключить, что p = 11 максимизирует прибыль. Поскольку это участок с высокими ценами, продукцию будут покупать только потребители из второй группы (5 баллов).

Обозначим месячную стоимость услуг провайдера за А. Пусть изначально сумма на счету равна B. Если не пользуемся скидкой и оплачиваем регулярно 12 раз в году, то сумма в конце года будет равна $$(B-A)(1+r)^{12}-A(1+r)^{11}-A(1+r)^{10}-...-A(1+r)$$ (2 балла).
По формуле суммы геометрической прогрессии это выражение равно $$B(1+r)^{12}-\frac{(1+r)^{13}-(1+r)}{r}$$(1 балл).
Если пользуемся скидкой, то сумма на счёте в конце года будет равна $(B-(1-s)12A)(1+r)^{12}$ (3 балла).
Остаётся сравнить два полученных выражения, А и B сократятся. Cогласиться на предложение будет выгодно, если
$$12(1-s) \leq \frac{(1+r)^{12}-1}{r(1+r)^{11}}$$ (3 балла)
Строгость или нестрогость знака значения не имеет. Преобразовав, получим ответ:
$$s \geq 1- \frac{(1+r)^{12}-1}{12r(1+r)^{11}}$$
(1 балл).

Производственные функции можно записать, как $x=(1+0.02n)2L_x$ и $y=(1+0.02n)4L_y$ (по 2 балла за каждую производственную функцию). Весь труд будет использоваться, т. к. все функции монотонно возрастают, поэтому $L_x+L_y+n=100$ (1 балл за уравнение):
$$\frac{x}{2(1+0.02n)}+\frac{y}{4(1+0.02n)}+L_n=100
\\y=4(1+0.02n)(100-n)-2x$$
(2 балла за уравнение).
Мы получили уравнение, описывающее доступные комбинации x и у при разных значениях $L_n.$ Чтобы получить уравнение КПВ, нужно сделать так, чтобы для каждого значения x значение $y=4(1+0.02n)(100-n)-2x$ было максимальным. Видно, что наклон этой линии не зависит от Ln, поэтому разные значения этого параметра задают параллельные друг другу прямые, из которых нам нужно выбрать самую высокую. Для этого нужно максимизировать функцию $(1+0.02n)(100-n)$. Это квадратичная парабола с ветвями вниз и корнями −50 и 100, значит, вершина параболы – точка максимума – будет находиться в точке 25 (посередине между корнями). Если $n=25$, то КПВ будет иметь вид $y=450-2x$ (3 балла).

В случае, когда есть две однородные группы, кривая Лоренца выглядит так:

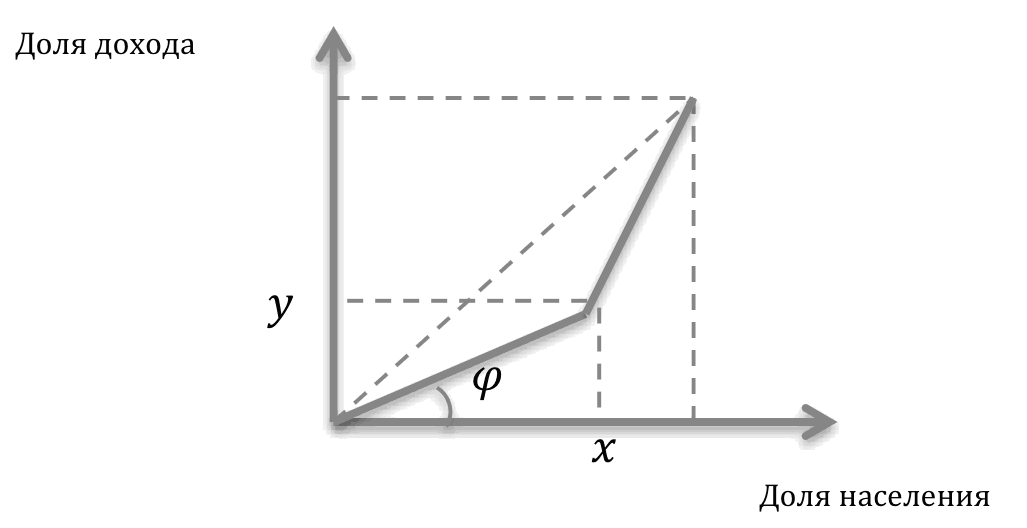
Вопрос задачи заключается в том, чтобы найти тангенс угла, обозначенного на рисунке как $\varphi $. На рисунке x – это доля бедных, а y – это доля доходов бедных.
Сначала поясним, как найти индекс Джини, зная долю доходов бедных и долю их численности.
Площадь под кривой Лоренца равна
$$0.5xy+0.5(y+1)(1-x)=0.5(y-x+1)$$ (2 балла).
Площадь между кривой равномерного распределения доходов и кривой Лоренца:
$$0.5-0.5(y-x+1)=0.5(x-y)$$ (2 балла).
Таким образом, индекс Джини равен: $G=\frac{0.5(x-y)}{0.5}=x-y$ (2 балла).
По условию задачи $G_A=2G_B; \ y_B=3y_A; \ x_B=2x_A$.
Тогда $\frac{x_A-y_A}{x_B-y_B}=2$(2 балла).
Находим $\tan \varphi =\frac{y_A}{x_A}=\frac{2\cdot 2 -1}{2\cdot 3 -1}=0.6$ (2 балла).

Обозначим месячную стоимость услуг провайдера за А. Пусть изначально сумма на счету равна B. Если не пользуемся скидкой и оплачиваем регулярно 12 раз в году, то сумма в конце года будет равна $$(B-A)(1+r)^{12}-A(1+r)^{11}-A(1+r)^{10}-...-A(1+r)$$ (2 балла).
По формуле суммы геометрической прогрессии это выражение равно $$B(1+r)^{12}-\frac{(1+r)^{13}-(1+r)}{r}$$(1 балл).
Если пользуемся скидкой, то сумма на счёте в конце года будет равна $(B-(1-s)12A)(1+r)^{12}$ (3 балла).
Остаётся сравнить два полученных выражения, А и B сократятся. Cогласиться на предложение будет выгодно, если
$$12(1-s) \leq \frac{(1+r)^{12}-1}{r(1+r)^{11}}$$ (3 балла)
Строгость или нестрогость знака значения не имеет. Преобразовав, получим ответ:
$$s \geq 1- \frac{(1+r)^{12}-1}{12r(1+r)^{11}}$$
(1 балл).

Производственные функции можно записать, как $x=(1+0.02n)2L_x$ и $y=(1+0.02n)4L_y$ (по 2 балла за каждую производственную функцию). Весь труд будет использоваться, т. к. все функции монотонно возрастают, поэтому $L_x+L_y+n=100$ (1 балл за уравнение):
$$\frac{x}{2(1+0.02n)}+\frac{y}{4(1+0.02n)}+L_n=100
\\y=4(1+0.02n)(100-n)-2x$$
(2 балла за уравнение).
Мы получили уравнение, описывающее доступные комбинации x и у при разных значениях $L_n.$ Чтобы получить уравнение КПВ, нужно сделать так, чтобы для каждого значения x значение $y=4(1+0.02n)(100-n)-2x$ было максимальным. Видно, что наклон этой линии не зависит от Ln, поэтому разные значения этого параметра задают параллельные друг другу прямые, из которых нам нужно выбрать самую высокую. Для этого нужно максимизировать функцию $(1+0.02n)(100-n)$. Это квадратичная парабола с ветвями вниз и корнями −50 и 100, значит, вершина параболы – точка максимума – будет находиться в точке 25 (посередине между корнями). Если $n=25$, то КПВ будет иметь вид $y=450-2x$ (3 балла).

Эластичность функции спроса постоянна, поэтому она задаётся уравнением $Q=k\cdot P$. В равновесии продаётся 10 единиц товара, поэтому k = 1 (так как
на кривой есть точка Q = P = 10).
1) Когда вводится потоварный налог на покупателей, можно сказать, что уравнение спроса будет описываться так: $Q=20-(P+t)=20-P-t$
$$Q^S=P
\\20-t-Q=Q
\\Q=0.5(20-t)$$
Налоговые сборы вычисляются по формуле:
$$T=t\cdot Q=0.5t(20-t)$$
Это парабола с ветвями вниз, поэтому есть максимум в вершине:
$$t^* =10$$
$T=0.5\cdot 10\cdot 10=50$ (3 балла).
2) Когда вводится налог на выручку, меняются стимулы каждой фирмы. Теперь каждая фирма максимизирует функцию прибыли:
Тогда в оптимуме
Тогда уравнение новой кривой предложения будет иметь вид: $P\cdot(1-t)=Q$
$$Q=20-P
\\Q=\frac{1-t}{2-t}\cdot 20$$
Тогда налоговые сборы вычисляются по формуле: T=tPQ (3 балла).
Сделаем замену переменных. Введём параметр k. Параметр $k=P^d-P^s$.
С другой стороны, k=t\cdot P
Тогда имеет место равенство $20-Q-k=Q$ Или $Q=0.5/(20-k)$
В таком случае максимизируем функцию $0.5k/(20-k)$
Аналогично пункту 1) оптимальным является k = 10
P = 15.
$$k=t\cdot P
\\ 10=t\cdot 15$$
$t^*=2/3$ или же $66\frac{2}{3}\%$.
Можно решать и без замены переменных, просто максимизируя функцию налоговых сборов.
У пункта есть и более простое решение. Поскольку ясно, что любой налог
в процентах от выручки − это эквивалент какого-то потоварного налога, найдём, какой процент от цены покупателя составляет старый налог. Цена покупателя была P = 20 − Q = 15, старый налог вводился по ставке 10, значит, эквивалентный адвалорный налог составляет 2/3 от выручки (66,(6) %).
Сумма налоговых сборов аналогично пункту 1) равна 50 (3 балла).
3) Безразлично (1 балл).

Обозначим зарплату Гены за Y. Если он десять месяцев будет откладывать по четверти своей зарплаты, то в итоге он получит сумму, равную $\dfrac{Y}{4}\cdot 10=2{,}5Y$. (2 балла)
Если Гена будет откладывать четыре месяца по половине зарплаты, то в итоге он накопит $\dfrac{Y}{2}\cdot 4=2Y$. Затем эту сумму Гена вложит в банк на два месяца и по истечении срока получит $2Y\cdot (1+0{,}12)^2 =2{,}5088Y$. (4 балла).
Действительно, сумма во втором случае очевидно больше суммы в первом случае. Вычтем одно из другого. Получим: $2{,}5088Y-2{,}5Y=0{,}0088Y$ (1 балл). Этого хватает ровно на одно мороженое, которое, по условию, стоит 88 медяков. Исходя из этого, можем подсчитать зарплату крокодила Гены:
$$\begin{equation}0{,}0088Y=88 \\ Y=\dfrac{88}{0{,}0088}=10000\end{equation}$$
Следовательно, зарплата Гены составляет 10 000 медяков (3 балла).

Пусть Х – цена двухлитровой упаковки сока, причём по этой цене оплачивается всего 1,5 литра сока, поскольку ¼ часть от двух литров покупатель получает
в подарок. Тогда цена одного литра сока (или сока в литровой упаковке) составляла Х/1,5 (2 балла).
После введения тотальной распродажи цена литровой упаковки сока снижается до 0,7Х/1,5 (1 балл).
Поскольку Вася, покупая 2 литра сока, экономит 6 рублей, (5 баллов), откуда находим, что Х = 90 (2 балла).

Пусть спрос задан уравнением $Q^D =a-b\cdot P$
Исходя из условия, мы можем составить два уравнения:
1) Равновесие при цене 5 долларов: $3+2\cdot 5=a-b\cdot 5$(4 балла).
2) Избыток при цене 7 долларов: $3+2\cdot 7-(a-b\cdot 7)=10$ (4 балла).
Решая эту систему, получаем, что $Q^D=28-3P$ (2 балла).

1) Заметим, что составитель А, составляя одну задачу для 11-го класса, отказывается от составления двух задач для 9-го. То есть для максимизации количества задач ему следует делать лишь задачи для 9-го класса. Аналогичным образом рассуждая, получим, что Б следует составлять только задачи для 7‒8-го класса. Тогда получим, что наибольшее число возможных задач равно $10 + 15 = 25 $(4 балла).
2) Да, они справятся с поставленной целью. Составителю А следует сделать 10 задач для 9-го класса, а составитель Б должен сделать одну задачу для 9-го класса и 11 задач для 7–8-го. Покажем, что каждый из них справится с этой работой. Для составителя А в условии указано, что он может справиться
с составлением 10 задач для девятиклассников.
Для составителя Б КПВ задаётся уравнением $y = 15 – 3x$. Где х – задачи для
9-го класса, у – для 7–8-го. Подставим $x = 1$. Получим $у = 12$. То есть составитель Б может сделать одну задачу для 9-го класса и 12 задач для 7–8-го. Другими словами, и 11 задач для 7–8-го он запросто сделает (6 баллов).

Пусть $K_x$ – количество единиц капитала, пущенного на производство икса,
$K_y$ – количество единиц капитала, пущенного на производство игрека,
$L_x$ – количество единиц труда, пущенного на производство икса,
$L_y$ – количество единиц труда, пущенного на производство игрека,
$L_k$ – количество единиц труда, пущенного на производство капитала.
Производственные функции: $x=\min\{K_x ; L_x /2 \}$, $y=\min\{K_y /2 ; L_y \}$ , кроме того, $K=K_x+K_y=2L_k$ (3 балла за равенство). Очевидно, что при эффективном использовании ресурсов будут справедливы равенства $x=K_x=L_x /2$ и $y=K_y/2=L_y$ (по 1 баллу за каждое равенство). Плюс добавится очевидное уравнение $L_x+L_y+L_k=100$ (2 балла за равенство). Составим систему:
$$\begin{cases}
x=K_x\\
x=L_x/2\\
y=K_y/2\\
y=L_y\\
K_x+K_y=2L_k\\
L_x+L_y+L_k=100
\end{cases}$$
Из этой системы будет получено уравнение, которым задаётся КПВ. Будем по очереди исключать из системы все переменные, кроме икса и игрека. Начнём с $K_x$ и $L_y$:
$$\begin{cases}
x=L_x/2\\
y=K_y/2\\
x+K_y=2L_k\\
L_x+y+L_k=100
\end{cases}$$
Теперь избавимся от $L_x$ и $K_y$:
$$\begin{cases}
x+2y=2L_k\\
2x+y+L_k=100
\end{cases}$$
Остаётся выкинуть $L_k$:
$x+2y=2(100-2x-y)$
$ x+2y=200-4x-2y$
$5x+4y=200$
$ y=50-1.25x$
(3 балла за вывод кривой производственных возможностей).

Обозначим функцию спроса: $Q_d=a-b\cdot P$.
Функция предложения: $Q_s=c+d\cdot P$.
Обозначим равновесную цену, как $P^*$.
Из условия задачи, что «при увеличении цены на литр молока величина спроса уменьшится ровно на столько же, на сколько увеличится величина предложения», следует, что $b=d$ (1 балл).
Когда цена в два раза больше, то никто не покупает молоко. Из этого следует, что:
$$ a-b\cdot2P^* =0
\\ a=2bP^* $$
(2 балла)
К тому же на рынке наблюдается избыток продукции:
$$Q_S-Q_D=10
\\c+d\cdot P-0=10
\\c+b\cdot2P^*=10
\\c=10-2bP^*=10-a$$
(2 балла)
Если цена в два раза меньше равновесной, то:
$$Q_S-Q_D=5
\\ a-b\cdot \frac{P^*}{2}-c-d\cdot \frac{P^*}{2}=5
\\ a-b\cdot \frac{P^*}{2}-10+a-b\cdot \frac{P^*}{2}=5
\\bP^*=5
\\a=10
\\c=0$$

(2 балла за верные вычисления).

То есть функция предложения проходит через центр координат. Вычислим размер дефицита, когда цена на молоко равна нулю: $10-b\cdot 0 - 0=10$.
Поскольку угол наклона функции спроса противоположен углу наклона функции предложения, то равновесная величина спроса и предложения будет равна 10/2 = 5 тыс. литров молока (можно показать на графике равнобедренный треугольник) (3 балла).

1) Сложим кривые предложения: $Q^H+Q^F=P+(-20+2P)=-20+3P$ при P>10. Запишем системой:
$$\begin{cases}
P, \ если \ 0 < P < 10 \\
-20+3P, \ если \ P \leq 10
\end{cases}$$
Найдём равновесие:
$$Q^S=Q^D; -20+3P=120-3P \rightarrow P=28, \ Q^S=64, \ Q^H=28, \ Q^F=36$$ .
Кроме того, участник должен сделать проверку того, что спрос пересекает предложение на этом участке (5 баллов).
2) Теперь рыночное предложение: $Q=P$
Равновесие:
$$Q^S=Q^D; \ p=120-P; \ P=40, \ Q^S=Q^H=40$$
После введения данной меры потребители Запутанной страны стали потреблять меньше скрепок и цена скрепок увеличилась. То есть они проиграли от данной меры. Производители Запутанной страны стали производить больше товара по более высокой цене, то есть они выиграли от введения данной меры (5 баллов).

1) Заметим, что составитель А, составляя одну задачу для 11-го класса, отказывается от составления двух задач для 9-го. То есть для максимизации количества задач ему следует делать лишь задачи для 9-го класса.

Аналогичным образом рассуждая, получим, что Б следует составлять только задачи для 11-го класса. Тогда получим, что наибольшее число возможных задач равно 10 + 15 = 25. (3 балла).
2) Да, они справятся с поставленной целью. Составителю А следует сделать 10 задач для 9-го класса, а составитель Б должен сделать одну задачу для 9-го класса и 11 задач для 11-го. Покажем, что каждый из них справится с этой работой. Для составителя А в условии указано, что он может справиться
с составлением 10 задач для девятиклассников.
Для составителя Б КПВ задаётся уравнением y = 15 – 3x. Где х – задачи для
9-го класса, у – для 11-го. Подставим x = 1. Получим у = 12. То есть составитель
Б может сделать одну задачу для 9-го класса и 12 задач для 11-го. Другими словами, и 11 задач для 11-го он запросто сделает (3 балла).
3) Б может обменивать одну задачу для 11-го класса на одну задачу для 9-го класса. То есть ему выгодно произвести 15 задач для 11-го класса и обменивать их все.
График при этом выглядит следующим образом (серая область – достижимые количества соответствующих задач, а чёрной линией отмечено первоначальное ограничение составителя Б):