К Рахманинову Вася не будет готовиться, поэтому Х+Y=7 и Х=7-Y
Итоговый средний по двум произведениям балл равен 1/2(11-Y)+1/2(3+2$\sqrt{Y}$)
Для нахождения максимума функции сделаем замену Z = $\sqrt{Y}$ , тогда
1/2(11-Z²)+1/2(3+2Z)
Парабола ветви виз, поэтому только один максимум в вершине параболы при Z = 1. Значит, Х= 6, Y= 1

Обратная кривая спроса на услуги автосалона в каждом районе имеет вид:
P(Q)=a-bQ, где $a_с = 2500$ и $a_Ю = 3000$ , а $b_Ю > b_c$ по условию задачи, поскольку спрос в районе Северный более чувствителен к изменению цены, чем в районе Южный, т.е. одинаковое изменение цены в каждом из районов приводит к более значительному изменению объема спроса в районе Северный, чем в районе Южный.
Средние издержки каждого из районов постоянны и равны 1500 рублей за нормочас, поэтому издержки предпринимателя имеют вид TC(Q)=AC(Q)*Q = 1500Q.
Так как Апполинарий – монополист в каждом из районов, задача максимизации его прибыли имеет вид:
$\Pi=P_ю(Q_ю)+P_с(Q_с)-TC(Q_ю+Q_c) \rightarrow max$ , где выбираются объемы продаж в Южном и Северном районах.
Поскольку издержки предпринимателя линейны, то задача максимизации совокупной прибыли может быть разбита на две независимые задачи (заметим, что если бы средние издержки монополиста были бы не постоянны, то разбиение задачи монополии на две независимые задачи максимизации прибыли в каждом из районов могло быть неправомерным!):
$P_ю(Q_ю)-1500Q_ю \rightarrow max$, где выбирается только $Q_Ю$, и
$P_с(Q_с)-1500Q_c \rightarrow max$, где выбирается только $Q_c$.
При условии линейности обратной функции спроса, график функциональной зависимости прибыли от объёма продаж является параболой, ветви которой направлены вниз, что гарантирует максимум прибыли в точке: $Q_ю=\frac{a_ю-1500}{2b_ю}$ и $Q_c=\frac{a_c-1500}{2b_c}$. Откуда можно найти цены за нормочас, которые будут установлены в каждом из районов, подставляя найденные объемы продаж в обратные функции спроса: $P_ю=\frac{a_ю+1500}{2}$= 2250 рублей за нормочас и $P_c=\frac{a_c+1500}{2}$= 2000 рублей за
нормочас.
Следует заметить, что при линейных обратных функциях спроса и постоянных предельных издержках монополиста цена, установленная в каждом из районов зависит только от величины предельных издержек и цены, при которой исчезает спрос на продукцию монополиста. Поэтому цена за нормочас будет выше в районе Южный, чем в районе Северный.

Критерии оценивания решения:

Записаны функции спроса в каждом из районов – по 2 балла за каждую функцию.
Верно выписаны издержки монополиста или его предельные издержки – 3 балла.
Верно составлена задача монополиста – 5 баллов.
Обосновано, что найденное значение цены или объёма продаж гарантирует
максимум прибыли – 2 балла.
Верно найдены цены монополиста в каждом районе – 4 балла.
Приведено верное сравнение цен – 2 балла.

Часто встречающаяся ошибка в решении: совершалась попытка сравнения цен монополиста, используя эластичности спроса по цене, при этом совершенно упускался тот факт, что для линейной кривой спроса эластичность не является величиной постоянной и зависит от того, в какой точке она была вычислена.

А) (10 баллов)
Последствия:
- Увеличение занятости за счёт увеличения национального производства
- Потери потребителей (рост цен при защите от импорта)
- Рост доходов национальных производителей, конкурирующих с импортом
- Рост доходов государственного бюджета
- Неэффективное использование ресурсов (перераспределение ресурсов из отраслей со сравнительным преимуществом)
- Высокая административная стоимость тарифной защиты
- Ослабление стимулов к НТП
- Непроизводительные расходы на лоббирование
- Опасность экономической войны между странами
- Падение цен факторов производства, интенсивно используемых в незащищаемых
отраслях, и рост цен в защищаемых.
Б) (10 баллов)
Цели:
• Рост доходов государственного бюджета
• Увеличение занятости
• Обеспечение безопасности государства.
• Защита молодых отраслей
• Защита потребителей от некачественных товаров
• Защита от дешёвой рабочей силы
• Защита от демпинга

Критерии оценки:
1) Полный балл (10 баллов) за ответ на каждый вопрос выставляется, если в ответе сформулировано больше двух корректных примеров и приведены объяснения, которые дают представления о понимании проблемы.
2) Если в ответе сформулированы два корректных примера и приведены пояснения, то выставляется 7 баллов.
3) Если в ответе сформулирован один корректный пример и приведены пояснения, то выставляется 4 балла (или 1 корректный пример и один не совсем точный).
4) Если в ответе сформулирован один корректный пример, но не приведены пояснения, то выставляется 2 балла.
5) Если содержание ответа не даёт представления о понимании проблемы, поставленной в вопросе, то участник получает 0 баллов.

А) В краткосрочном периоде спрос падает незначительно по нескольким причинам
- отсутствие других видов транспорта, кроме электрички, в результате уходят пассажиры, у которых нерегулярные поездки (гости и пр.);
- часть пассажиров пересядет на другие виды транспорта при их наличии (автобус, маршрутное такси и пр.). (5 баллов за одну из причин с объяснением)

Большая долгосрочная эластичность объясняется тем, что со временем у потенциальных пассажиров пригородного железнодорожного транспорта появляется возможность принять необходимые решения о покупке автомобиля, подборе попутчиков для совместных поездок на одном автомобиле или перемене места жительства и работы. (10 баллов за две корректные причины с объяснением)

Общие фразы о большем количестве товаров-заменителей в долгосрочном периоде по сравнению с краткосрочным периодом оценивались в 3 балла.

(5 баллов) Б) Прямая эластичность спроса по цене. (Если нет указания на вид эластичности, то выставляется 3 балла).

Составим таблицу производительности труда гномов.

Гном	До курсов
	Шары	Звездочки
Ори	1 шт./час	1 шт./час
Дори	3 шт./час	0 шт./час
Нори	2 шт./час	2 шт./час

А) Первый способ. «Аналитический»
Пусть T — общее время, затраченное гномами на работу, $l_О$ — время, затраченное Ори на изготовление шаров, а $l_Н$ — время, затраченное Нори на изготовление шаров. Поскольку шары делают только эти два гнома, верно неравенство
$$l_0+2l_H \ge 240$$
так как, по условиям контракта, должно быть изготовлено 240 шаров, но распределение времени в оптимуме может оказаться таким, что выпустить можно и больше шаров, чем нужно. Аналогично, звёздочек должно быть 120, так что
$$(T-l_0)+3T+2(T-l_H) \ge 240$$
Приводя подобные слагаемые и учитывая оба неравенства, получаем $T \ge 60$, откуда и получаем наименьшее затраченное время 60 часов.

Второй способ. «Графический»
Построим КПВ гномов в расчёте на один час:

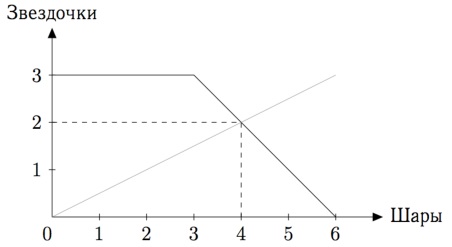
Чтобы шары и звёздочки были в правильной пропорции, нужно выбрать точку (4;2) на этой КПВ, то есть за час будет изготовлено 2 комплекта. Получаем, что 120 комплектов будет изготовлено за 60 часов.

Третий способ. «Оценка плюс пример»
Даже если каждый гном будет производить только то, что умеет делать лучше, гномам не удастся произвести более 6 украшений (любых типов) за час. В каждом комплекте 3 украшения, значит, произвести за час больше двух комплектов точно не удастся. Это означает, что 120 комплектов точно не будут сделаны быстрее, чем за 60 часов. Покажем, как сделать их ровно за 60 часов: Дори произведёт 180 шаров, Ори произведёт 60 звёздочек, а Нори произведёт 60 шаров и 60 звёздочек.

$S_N \ge S_0 \cdot Z$
В конце 1 года на вкладе будет сумма $S_1 = S_0 \cdot (1+\frac{i}{100})-D$
В конце 2 года на вкладе будет сумма
$S_2 = S_1 \cdot (1+\frac{i}{100})-D=(S_0 \cdot (1+\frac{i}{100})-D) \cdot (1+\frac{i}{100})-D=S_0 \cdot (1+\frac{i}{100})^2-D(1+(1+\frac{i}{100}))$
В конце 3 года на вкладе будет сумма
$S_3 = S_2 \cdot (1+\frac{i}{100})-D=S_0 \cdot (1+\frac{i}{100})^3-D(1+(1+\frac{i}{100})+(1+\frac{i}{100})^2)$
$S_N = S_0 \cdot (1+\frac{i}{100})^N-D(1+(1+\frac{i}{100})+(1+\frac{i}{100})^2+ \dots + (1+\frac{i}{100})^{N-1})$
Пусть $1+\frac{i}{100}=y$ и по формуле суммы геометрической прогрессии получим
выражение:
$1+(1+\frac{i}{100})+(1+\frac{i}{100})^2+ \dots + (1+\frac{i}{100})^{N-1})=1+y+y^2+ \dots +y^{N-1}=\frac{1-y^N}{1-y}$
$S_N=S_0\cdot y^N-D\cdot \frac{1-y^N}{1-y}$
$S_0\cdot y^N-D\cdot \frac{1-y^N}{1-y} \ge S_0Z$
$D \le (S_0y^N-S_0Z)\cdot \frac{1-y}{1-y^N}$
$D \le S_0(y^N-Z)\cdot \frac{1-y}{1-y^N}$
$D \le S_0((1+\frac{i}{100})^N-Z)\cdot \frac{1-(1+\frac{i}{100})}{1-(1+\frac{i}{100})^N}$

Составим таблицу производительности труда гномов.

Гном	До курсов		После курсов
	Шары	Звездочки	Шары	Звездочки
Ори	1 шт./час	1 шт./час	1 шт./час	2 шт./час
Дори	3 шт./час	0 шт./час	(3 + k) шт./час	0 шт./час
Нори	2 шт./час	2 шт./час	4 шт./час	2 шт./час

А) Первый способ. «Аналитический»
Пусть T — общее время, затраченное гномами на работу, $l_О$ — время, затраченное Ори на изготовление шаров, а $l_Н$ — время, затраченное Нори на изготовление шаров. Поскольку шары делают только эти два гнома, верно равенство
$$l_0+2l_H=240$$
так как, по условиям контракта, должно быть изготовлено 240 шаров. Вместе с тем, звёздочек должно быть 120, так что
$$(T-l_0)+3T+2(T-l_H)=240$$
Приводя подобные слагаемые и подставляя первое уравнение во второе, получаем T = 60.

Второй способ. «Графический»
Построим КПВ гномов в расчёте на один час:

Чтобы шары и звёздочки были в правильной пропорции, нужно выбрать точку (4;2) на этой КПВ, то есть за час будет изготовлено 2 комплекта. Получаем, что 120 комплектов будет изготовлено за 60 часов.

Третий способ. «Оценка плюс пример»
Даже если каждый гном будет производить только то, что умеет делать лучше, гномам не удастся произвести более 6 украшений (любых типов) за час. В каждом комплекте 3 украшения, значит, произвести за час больше двух комплектов точно не удастся. Это означает, что 120 комплектов точно не будут сделаны быстрее, чем за 60 часов. Покажем, как сделать их ровно за 60 часов: Дори произведёт 180 шаров, Ори произведёт 60 звёздочек, а Нори произведёт 60 шаров и 60 звёздочек.

Б) Заметим, что любая выручка, полученная с участием продажи комплектов, может быть получена и при продаже украшений только по отдельности (потому что комплект стоит столько же, сколько его части, проданные сами по себе). Поэтому в дальнейшем мы будем игнорировать возможность продажи комплектами, а будем обсуждать только продажу отдельных украшений.

• Как бы ни изменилась производительность Дори, ему есть смысл делать наибольшее возможное число шаров, чтобы максимизировать выручку (звёздочки он делать не умеет).
• Сделав шар, Ори может продать его за 50 монет. Вместо этого за то же время он может сделать две звезды и продать их за 140 монет. Значит, Ори делает только звезды.
• Сделав звезду, Нори может продать её за 70 монет. Вместо этого за то же время он может сделать два шара и продать их за 100 монет. Значит, Нори делает только шары.

Издержки фабрики на одного нанятого, есть зарплата женщин на фабрике, т.е. $w=0,5L+1$, что есть обратная функция предложения труда женщин в регионе.
При зарплате 5 тыс. рублей наняты будут все желающие работать женщины. Их численность можно узнать, подставив значение заработной платы в функцию предложения труда, т.е., $L= 2w − 1 = 8$. То есть, при поддержке региональных властей на фабрике было занято 8 сотен женщин.
В отсутствии финансирования фабрика Нить (монопсонист) решает следующую задачу максимизации своей прибыли:
$П =py(L)-w(L)*L \rightarrow max$, выбирая численность нанятых.
Подставляя данные, имеем:
$10L-0,25L^2-(0,5L+1)*L \rightarrow max$
График целевой функции является параболой, ветви которой направлены вниз, что гарантирует максимум в точке: $L^*= 6$ (сотен женщин).
Следовательно, монопсонист установит заработную плату на уровне
$L = 0,5 ∗ 6 + 1 = 4$ (тыс. рублей)
Откуда получаем, что заработная плата сократится на $\frac{5-4}{5}∗ 100\% = 20\%$, а
количество занятых в производстве женщин сократится на $\frac{8-6}{8}∗ 100\% = 25\%$

1. Использование протекционизма для защиты национальных рынков труда – сохранение рабочих мест в стране, борьба с безработицей для уменьшения социальной напряжённости.
2. Использование протекционизма в целях национальной безопасности – защита стратегически важных отраслей промышленности, снижение зависимости от импортных поставок сырья и товаров.
3. Использование протекционизма для развития отраслей, выпускающих уникальные продукты, которые можно экспортировать на внешние рынки, молодых отраслей и высокотехнологичных (интернализация внешнего эффекта).
4. Желание с помощью тарифов привлечь в страну иностранных производителей товаров (невыгодность ввоза готовой продукции из-за роста цен в результате ввода таможенных тарифов).
5. Возможность улучшить условия торговли (ценовые пропорции) путём установления импортных таможенных тарифов большой экономикой, которая способна влиять на формирование мировых цен.

Критерии оценивания:
1) Полный балл (20 баллов) выставляется, если в ответе сформулировано больше двух корректных примеров и приведены объяснения, которые дают представления о понимании проблемы.
2) Если в ответе сформулированы два корректных примера и приведены пояснения, то выставляется 7 баллов.
3) Если в ответе сформулированы два корректных примера, но не приведены пояснения, то выставляется 5 баллов
4) Если в ответе сформулирован один корректный пример и приведены пояснения, то выставляется 4 балла (или 1 корректный пример и один не совсем точный).
5) Если в ответе сформулирован один корректный пример, но не приведены пояснения, то выставляется 2 балла.
6) Если содержание ответа не даёт представления о понимании проблемы, поставленной в вопросе, то участник получает 0 баллов.

А) Экономика находится в состоянии долгосрочного равновесия, то есть в состоянии общего экономического равновесия при полной занятости. Процесс установления макроэкономического равновесия в долгосрочном периоде сводится к формированию равновесия на рынке труда и рынке благ. Равновесие на рынке труда предопределяет равновесие рынка благ. На рынке труда в результате взаимодействия спроса на труд с его предложением определяется уровень занятости, а следовательно, и объём предложения благ при заданной технологии.
1) Найдём равновесный уровень занятости на рынке труда.
Для этого сначала зададим функцию спроса агрегированной фирмы на труд из условия максимизации прибыли:
$Pr(L)=P* F(L)-W*L \rightarrow \max$
$Pr'(L)$
$P* F'(L)-W=0$; $F'(L)=\frac{50}{\sqrt{L}}$
$F'(L)-\frac{W}{P}=0$
$P*\frac{50}{\sqrt{L}}=W$
$L^D=\frac{2500}{(\frac{W}{P})^2}$

2) Найдём равновесный уровень занятости на рынке труда.
$L^D=L^S$
$\frac{2500}{(\frac{W}{P})^2}=20*\frac{W}{P}$
$\frac{W}{P}=5$
Равновесная реальная заработная плата равна 5. (2 балла)
Подставим эту величину либо в функцию спроса на труд $L^D$, либо в функцию предложения труда $L^S$:
L= 20*5=100 (1 балл)

3) Найдём объём предложения благ при заданной технологии:
$Y = F(L)=100*\sqrt{100} =1000$ - это объём выпуска в долгосрочном равновесии. (1 балл)

4) Величина совокупного предложения, т.е. потока всех благ, произведённых в стране за данный период, как и выпуск отдельной фирмы, определяется количеством ресурсов и используемыми в экономике технологиями. Поэтому уравнение кривой совокупного предложения в долгосрочном периоде
выводится из анализа рынка труда:
$Y^{AS}=1000$

5) Так как в долгосрочном равновесии все рынки находятся в равновесии, то приравняв функцию совокупного спроса к функции совокупного предложения найдём равновесный уровень цен в экономике. Функция совокупного спроса:
$Y^{AD}=\frac{MV}{P}=\frac{4×500}{P}=\frac{2000}{P}$
Равновесие на рынке благ:
$Y^{AD}=Y^{AS}$
$\frac{2000}{P}=1000$
$P_{LR} = 2$ (1 балл)
Ответ: $P_{LR} = 2$; $L = 100$; $W/P = 5$; $Y=1000$; $Y^{AS} =1000$

Б) (5 баллов)
1) Для ответа на вопрос найдём номинальную ставку заработной платы:
$W =\frac{W}{P}*P =5×2=10$ (1 балл)
2) В краткосрочном периоде номинальная ставка заработной платы не изменяется быстро в связи с контрактной системой.
При заданной номинальной ставке заработной платы объём спроса предпринимателей на труд зависит от фактической прибыли и фактического уровня цен. А спрос фирм на труд полностью определяет занятость в экономике. Фирмы будут нанимать работников после того, как узнают фактический уровень цен.
Подставим зафиксированную в трудовых контрактах номинальную ставку
заработной платы в функцию спроса на труд:
$L_D = \frac{2500}{( \frac{10}{P})^2}= 25*P^2$ (2 балла)
3) При заданной технологии функция совокупного предложения в краткосрочном периоде имеет вид:
$Y^{AS}=100*\sqrt{25*P ^2} =500*P$ (2 балла)
Ответ: $Y^{AS} = 500*P$

В) (6 баллов)
1) Новая функция совокупного спроса имеет вид:
$Y^{AD}= 2,25*\frac{500}{P}=\frac{1125}{P}$
2) Найдём макроэкономическое равновесие на рынке благ в краткосрочном периоде
после негативного шока, приравняв функцию совокупного спроса к функции
совокупного предложения:
$Y^{AD}=Y^{AS}$
$\frac{1125}{P}=500P$
$P_{SR}=1,5$ (2 балла)
$Y_{SR} =500*1,5=750$ (1 балл)
3) Найдём процентные изменения уровня цен и выпуска.
Темп инфляции в краткосрочном периоде:
$(\frac{P_{SR}}{P_{LR}}−1)*100\%=(\frac{1,5}{2}−1)×100\%=−25\%$ (1 балл)
Темп прироста выпуска в краткосрочном периоде:
$(\frac{Y_{SR}}{Y_{LR}}−1)×100%=(\frac{750}{1000}−1)×100\%=−25\%$ (1 балл)
4) В краткосрочном периоде в экономике будут наблюдаться спад производства (рецессия), рост уровня безработицы и дефляция. (1 балл)
Ответ:
- $P_{SR} = 1,5$; $Y_{SR} = 750$; темп прироста выпуска = (-25%); темп инфляции = (-25%)
- спад производства (рецессия), рост уровня безработицы и дефляция

Г) (4 балла)
1) Центральный банк, чтобы восстановить исходный уровень выпуска в экономике, будет проводить стимулирующую монетарную политику (политику «дешёвых денег»). (1 балл)

За счёт покупки облигаций на открытом рынке ЦБ увеличивает предложение денег в экономике.
Найдём на сколько ЦБ должен увеличить денежную массу, чтобы стабилизировать выпуск. Для этого подставим величину потенциального объёма выпуска в новую функцию совокупного спроса, где неизвестной величиной будет новая денежная масса:
$\frac{2,25*M_2^S}{2}=1000$
$M_2^S=\frac{2000}{2,25} \approx 888,89$
$\Delta M^S= M_2^S−M_1^S=888,89−500=388,89=\frac{3500}{9}$ (1 балл)
2) Найдём на какую сумму ЦБ должен выкупить облигации на открытом рынке, чтобы увеличить предложение денег на 388,89.
Изменение денежной базы в результате выкупа облигаций вызовет увеличение предложения денег в экономике за счёт мультипликативного эффекта. Из условия известно, что население не хранит деньги в виде наличности, норма обязательного резервирования составляет 4%, коммерческие банки не имеют избыточных резервов и полностью используют свои кредитные возможности. Поэтому денежный мультипликатор будет равен депозитному мультипликатору:
$mult =\frac{1}{rr}=\frac{1}{0,04}= 25$
$\Delta M^S= \Delta bonds*mult$
$\frac{3500}{9}= \Delta bonds×25$
$\Delta bonds\times\frac{140}{9}\approx 15,56$
(2 балла)
Ответ:
- цб будет проводить стимулирующую монетарную политику
- ЦБ необходимо выкупить облигации на сумму 15,56.

Сравнение двух возможностей: рыбачить по 4 часа и рыбачить по 8 часов. При рыбалке 4 часа каждый рыбак заработает 4*3*500+4*x, при рыбалке 8 часов каждый заработает 8*2*500. При x>500 вариант рыбачить 4 часа выгоднее. При x<500 вариант рыбачить 8 часов выгоднее.
За это решение - 25 баллов

За решение, при котором рассматривалась возможность индивидуального отклонения, то есть когда один из рыбаков рыбачит 8 часов, другой - 4 ч оценивалось за каждое сравнение по 10 баллов. Это решение включает в себя следующие сравнения. Условия рыбалки по 4 часа:
4*3*500+4*x>8*2,5*500;
x>1000.
Условия рыбалки по 8 часов:
8*2*500>4*2,5*500+4*x;
x<750.

Монополист максимизирует прибыль с учётом налога:
$$max_{Q \ge 0} [100Q-2Q^2-20Q-tQ]$$
Поскольку функция представляет собой параболу ветвями вниз, её максимум достигается в точке
$$Q^*=\frac{-80+t}{-4}=20-1/4t$$
Правительство знает, как поведёт себя фирма при введении налога, и с учётом этого устанавливает такой налог, который максимизирует сумму налоговых сборов
$$max_{t \ge 0} [Q*t]=max_{t \ge 0} [(20-1/4t)t]$$
Эта функция также является параболой ветвями вниз, и её максимум достигается в точке
$t^*=20$

Фирмы полагают, что выгоды от участия в картеле будут больше, нежели штраф, который они заплатят в результате доказательства сговора. Идёт речь о долгосрочном периоде. (10 баллов)

Основная выгода от участия в картеле – увеличение прибыли. (10 баллов при наличии объяснения)
Если все фирмы в отрасли объединяются в картель, то они начинают вести себя как монополия. Основная цель картеля состоит в максимизации прибыли. Так как картель определяет единую цену продаж, то каждая дополнительная единица продукта будет приносить одинаковую предельную выручку для каждой фирмы. В результате объем продаж будет определяться из равенства предельных издержек фирм между собой. Таким образом, происходит перераспределение прибыли между фирмами для компенсации сокращения объёма выпуска фирм в результате установления картелем квот продаж. Картель сокращает объем выпуска, что приводит к росту цены и совокупной прибыли фирм.
5 баллов выставляется
- либо за указание одного корректного примера дополнительных
выгод от участия в картеле с приведённым объяснением
- либо при указании на низкую вероятность наказания.

Дополнительные выгоды от участия в ценовых сговорах:
1. Закрепление некоторых сегментов рынка под монопольным контролем
2. Дезинформация потребителей (имитация конкуренции)
3. Совместная борьба с аутсайдерами (установление барьеров для входа в
отрасль)
4. Лоббирование интересов картеля в органах государственной власти
5. Фирмы могут сообщить о существовании картеля, будут освобождены от ответственности и получат конкурентные преимущества на рынке за счёт увеличения объёма продаж (правительства многих стран используют эту меру для борьбы с картелями – программы ослабления наказания).

Фирмы также считают, что вероятность обнаружения ценового сговора низка. Если фирмы-участницы картеля ожидают, что картельное соглашение будет вскоре обнаружено правительством, и последуют строгие санкции, фирмы будут менее склонны к заключению такого рода соглашений, и наоборот: чем ниже риск обнаружения картельного соглашения антимонопольными органами и использования строгих санкций, тем выше стимулы объединения и поддержания картеля.

Влияние на мобильность:

1) Доступность ресурсов и цивилизованных благ (больницы, магазины, работа и образование)
2) Активность населения
3) Улучшение финансового положения (рост заработной платы, увеличение использования транспорта людьми с низкими доходами позволяет им увеличить расходы на другие нужды, нет расходов на аренду автомобиля)
4) Возможность совершать социально-ориентированные поездки (гости и пр.)

Влияние на показатели рынков:
1) Рынок труда – уменьшение дифференциации заработной платы между регионами страны, централизация рынка труда в местах прибытия, концентрация в нем востребованных кадров и нарастание перемещений маятникового характера, рост производительности труда в местах прибытия, присоединение обширных территорий к зонам трудовой занятости, более равномерное распределение трудовых ресурсов;
2) Рынок транспортных услуг и инфраструктуры – сокращение количества используемых автомобилей, снижение нагрузки на улично- дорожную сеть, сокращение затрат на строительство автодорог и парковок. В результате сокращаются выбросы в атмосферу и потери здоровью, время поездок на работу (заторы).
3) Рынок недвижимости – изменение стоимости недвижимости (может как вырасти при появлении станции или упасть из-за внешних эффектов – шум, вибрация, скопление автомобилей вокруг станций, ухудшение привлекательности ландшафта для туристов).
4) Рынок образования – рост спроса в местах прибытия.
5) Рынок автомобилей – сокращение спроса (и на бензин).
6) Влияние на другие рынки оценивалось при наличии корректного объяснения.

Критерии оценивания:
1) Варианты влияния на мобильность оценивались максимально в 10 баллов.
2) Варианты влияния на рынки максимально оценивались в 15 баллов, из них в 5 баллов оценивалась идея о расширении географических границ рынков товаров, услуг, факторов производства.

1) Полный балл (10 баллов) выставляется, если в ответе сформулировано больше двух корректных примеров и приведены объяснения, которые дают представления о понимании проблемы.
2) Если в ответе сформулированы два корректных примера и приведены пояснения, то выставляется 7 баллов.
3) Если в ответе сформулирован один корректный пример и приведены пояснения, то выставляется 4 балла (или 1 корректный пример и один не совсем точный).
4) Если в ответе сформулированы два корректных примера, но не приведены пояснения, то выставляется 5 баллов
5) Если в ответе сформулирован один корректный пример, но не приведены пояснения, то выставляется 2 балла.
6) Если содержание ответа не даёт представления о понимании проблемы, поставленной в вопросе, то участник получает 0 баллов.